УДК 621.744

В. С. Дорошенко

Информация передана для публикации на o8ode.ru автором - контакты - dorosh@inbox.ru.

В данном разделе - 4 статьи об изделиях изо льда, который тает (талая вода в большинстве способов отверждает близлежащую песчаную смесь), и затем на его месте возникает отливка из металла.

Физико-технологический институт металлов и сплавов НАН Украины

Формирование структуры литейной ледяной модели и методы его моделирования

Состав и структура материала литейной одноразовой ледяной модели во многом определяют качество этой модели и полученной по ней отливки, поскольку этот материал в дальнейшем используют при изготовлении литейной песчаной формы. Поэтому важно понимать механизм и кинетику затвердевания льда при получении модели, распределение в нем примесей. Рассмотрены современные  модели кристаллизации с учетом теории кластеров и фракталов, приведены примеры моделей.

 Ключевые слова: литейные ледяные модели, водная композиция, дендриты, кластеры, фракталы.

            Разработка новых видов криотехнологии для литейного производства дает возможность повысить его экологическую чистоту путем замены традиционных полимерных модельно-формовочных материалов замороженной водой. Литье по ледяным моделям (ЛЛМ), внедряясь с этой целью в область точного литья - ЛГМ и ЛВМ, в процессе разработки технологии изготовления моделей позволяет заметить некоторые характерные закономерности, свойственные явлениям кристаллизации и являющиеся важными для создания качественных литейных моделей с разнообразными технологическими свойствами. Прозрачность льда давно используют для облегчения визуального наблюдения структурообразования и строения дендритов при физическом моделировании процессов кристаллизации металлов, полимеров и т. п. Отмеченные авторами особенности кристаллизации льда при охлаждении воды до температур минус 15…20°С, современные варианты его моделирования, а также использование результатов исследований для производства литейных ледяных моделей составляют тему этой статьи.

            Для производства описанных в статье образцов ледяных моделей применяли чистую водопроводную воду, а также водную композицию с технологическими добавками до 25% связующих с целью последующей частичной пропитки песка образуемой вокруг ледяной модели литейной формы при таянии этой модели. В некоторых вариантах в материал модели или ее облицовку вводили мелкодисперсный бентонит или огнеупорный наполнитель – дистен-силлиманит с целью создания противопригарных свойств поверхности этой песчаной формы. Подробности формовки описаны в работе [1]. В большинстве разрабатываемых разновидностях ЛЛМ одноразовые модели после помещения их в песок литейной формы подлежат плавлению с удалением избытка жидкости из полости формы, в т. ч. при частичном испарении подсушкой при помощи вакуумирования формы. Поэтому нет необ-ходимости их сильного охлаждения, вполне достаточно температуры минус 15...20⁰ С.

            Анализ последних публикаций не выявил исследований структуры промышленных конструкций изо льда, однако аналогичные явления рассмотрены в структурной криологии [2] и мерзловедении [3], которые изучают кристаллы льда преимущественно как материальную основу криосферы нашей планеты. В связи с этим заметим, что оборот материала ледяных моделей с его таянием и частичным испарением на литейном участке в какой-то мере заимствует черты (подобно микрокопии) кругооборота воды в природе нашей планеты, который является глобальной системой переноса, поддерживающей энергои экологический глобальной системой переноса, поддерживающей энергои экологический баланс всей Земли.  Пожалуй, кроме воды не имеется других природных материалов, которые могут  находиться в твердом, жидком и газообразном состоянии в узком интервале температур +20...-20⁰ С.

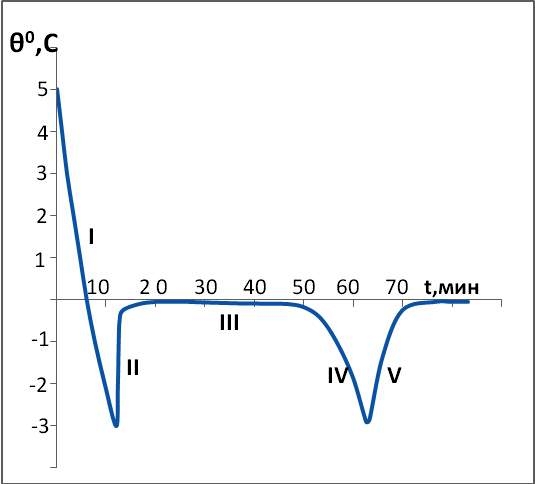
            В последней упомянутой работе, которую считают классической в этой области, приведены эксперименты по замораживанию водонасыщенных образцов характерных типов грунтов, в частности песка и бентонита. Методика состояла в том, что грунт замораживали в пробирке, погруженной в замораживающую смесь с температурой -10⁰ С в сосуде Дюара. Температуру θ охлаждения и замерзания грунта записывали на фотобумаге с помощью зеркального гальванометра (рис. 1).

                                    а)                                                            

 б)

Рис. 1 Кривые охлаждения: а – песка влажностью W=19,6%; б – дисперсной бентонитовой глины влажностью W=80,5%.

На рис.1а кривая замерзания водонасыщенного люберецкого кварцевого песка состоит из нескольких участков. Участок (I) соответствует только понижению температуры образца в процессе охлаждения и переохлаждения, наибольшая температура которого достигала θ = -3⁰С. В образце начинает замерзать вода и выделяется такое количество скрытой теплоты льдообразования, что температура грунта резко повышается до ~0⁰С (участок II, рис. 1а). При этой температуре в водонасыщенном образце происходит замерзание всей свободной воды, причем время замерзания зависит от влажности композиции, интенсивности охлаждения и размеров образца. Далее следует участок, характеризирующийся стабилизацией температуры на уровне 0⁰С, которая соответствует температуре замерзания грунта. Если продолжать замораживать образец, то по прошествии некоторого времени температура его начнет понижаться – вначале по криволинейному закону. Выпуклость кривой к оси температур показывает, что на участке все еще продолжает выделяться скрытая теплота льдообразования и замерзает рыхлосвязанная (переменного фазового состава) вода. Однако при температуре ниже  -1^{0 С} охлаждение идет по прямолинейному закону (участок IV, рис. 1а), можно считать состояние песка замершим, т.е. в нем практически вся вода перешла в лед. При повышении температуры (участок V) сначала температура изменяется прямолинейно, а затем криволинейно – скрытая теплота льдообразования начинает поглощаться, еще не достигнув температуры таяния образца.

Все сказанное относится и к глинистым образцам (рис. 1б). Основное отличие состоит в том, что после температурного скачка устанавливается более низкая температура (-0,1…-2,5 ⁰С) и кривая участка стабилизации температуры выглядит покатой. Это вызвано явлением набухания (мицелообразования) частиц глины, которое приводит к частичному связыванию воды, а также может быть следствием некоторого повышения концентрации солей в воде. Для криотехнологий литейного производства правомерна аналогия в том, что замораживание рассмотренных песчаного образца сравнимо с процессами получения замороженной песчаной формы, а водонасыщенного глинистого образца – с получением ледяной модели при замораживании водной композиции в пресс-форме.  

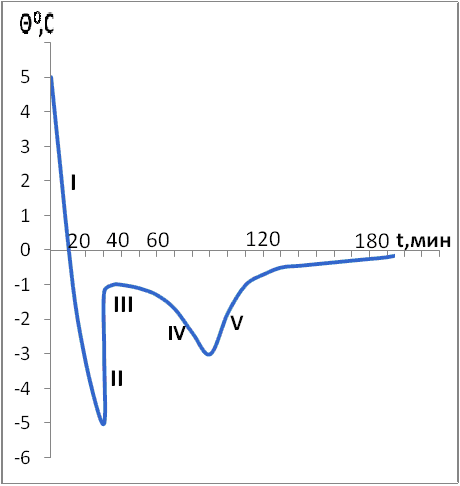
Для исследования процесса замораживания водной композиции на образцах значительно большей массы в условиях, свойственных опытному производству литейных моделей, во ФТИМС НАНУ провели измерения температуры при охлаждении образцов в воздушной среде внутри морозильной камеры с температурой –(15…17)⁰С. Замораживали в цилиндрическим сосуде диаметром 100 мм из гибкого тонкостенного пластика три вида образцов массой по 1 кг: из водопроводной воды, а также водные композиции с связующими компонентами, 25%-й раствор жидкого натриевого стекла (плотностью 1,08 г/см³) и 25%-й раствор декстрина (плотностью 0,98 г/см³). Температуру определяли в центре образца, начальная температура была +3⁰С.

Рис. 2. График замораживания водных образцов с различными компонентами.

Анализ кривых показывает, что все три образца начали охлаждаться одновременно спустя 5 минут помещения их в морозильную камеру. Охлаждение жидкостекольной композиции шло несколько быстрее двух других из-за повышенной теплопроводности. На графиках видно, что постепенное понижение температуры сменяется небольшими горизонтальными участками. Первые «полки» кривых слева вблизи 0⁰С связаны с переходом воды из жидкого состояния в твердое, при котором происходит выделение скрытой теплоты льдообразования. Поскольку в центре образца жидкость замерзала в последнюю очередь, то ее температура до замерзания фиксировалась на доли градуса выше 0⁰С. Некоторое нарушение плавного хода кривых, если это отражалось на них синхронно, мы связываем с периодичностью включения-выключения компрессора камеры, с процессами внутри растворов, либо погрешностью измерений. Полученные зависимости показали, что композиция с добавкой жидкого стекла закристаллизовалась за 30…32 мин., что быстрее двух других, которые затвердели примерно в одно и то же время 40…45 мин. Энергозатраты морозильника Nord-155 объемом 200 л при часовом расходе электроэнергии не более 0,06 кВт.ч для поддержания температуры в камере до -18⁰С при охлаждении 1 кг льда до измеренной температуры -11…-12⁰С за 3 часа составляют не более 0,18 кВт.ч. Или для литья железоуглеродистых сплавов – 25,7 кВт.ч на 1 т отливок,  что можно сравнить с данными В. С. Грузмана – 59,5 кВт.ч  на 1 т стальных отливок при литье в замороженную форму, охлажденную до -30⁰С, а также можно использовать для расчета производительности морозильных камер при получении моделей в опытном производстве.

Для моделирования процесса кристаллизации водного раствора при получении ледяной модели кратко напомним некоторые известные положения, подробнее рассмотренные в недавних публикациях [2, 4, 5]. Этот процесс начинается с выделения из переохлажденного раствора зародышей кристаллов, и последующая кристаллизация протекает при дальнейшем охлаждении раствора на образовавшихся зародышах. Получение в процессе кристаллизации крупных кристаллов свидетельствует, что количество зародышей, образующихся в первый момент, было относительно небольшим, поскольку распределение вновь выделяющихся кристаллов при охлаждении раствора на большом числе зародышей приводит к образованию мелких кристаллов. Чем выше скорость охлаждения, тем больше таких кристаллических зародышей образуется в растворе и тем меньшим будет размер образовавшихся кристаллов. Скорость роста кристаллов V (в г/сек) на образовавшихся центрах кристаллизации И. И. Андреевым предложено определять уравнением [5]:

                                    V = dx/dt = kS(x - х'),

где dx/dt - количество вещества, закристаллизовавшегося в единицу времени; k — коэффициент, зависящий от диффузии молекул, достигших температуры затвердевания (d), и средней длины диффузионного пути (δ); k = d / δ; S — поверхность выделившейся твердой фазы; х — концентрация переохлажденного раствора; х' — растворимость зародышей кристаллов при данной степени их дисперсности.

Механизм возникновения роста кристаллов льда в воде наиболее адекватно отражает кластерная модель, предложенная X. Фрэнком, В. Уэном в 1957 г. [2]. Согласно этой модели жидкая вода является конгломератом крупных ассоциатов молекул Н₂О (кластеров), возникающих и вновь распадающихся. Представление о льдоподобном строении таких «мерцающих» кластеров основано на рентгеновских и инфракрасных исследованиях воды, которые показали, что расположение молекул внутри кластеров похоже на расположение их в кристаллической решетке льда. Понижение температуры приводит к увеличению молекул в кластере. При температype 65^оС среднее число молекул в кластере составляет 15...50 единиц, при 0°С — 90...120 и достигает 150...180 единиц при температуре - 20°С (Голубев, 1999). Таким образом, по этой модели еще до формирования первых устойчивых кристаллов льда (рис. 3 а) в воде существуют льдоподобные образования [2].

Рост кристаллов льда происходит не постоянно как результат отложения на гранях отдельных молекул, а скачками, за счет присоединения отдельных блоков размером примерно 10^-7 – 10^-3 см. Это вызывает в отдельных микроблоках изменение кристаллографических осей <С> и <а> на несколько угловых минут и даже градусов. В кристаллах, образующихся в условиях переохлаждения до -10°С, разориентация отдельных блоков достигает 1-3 угловых градусов, а в случае малых переохлаждений такая разориентация не превышает долей градуса. Механизм кластерного роста, однако, не исключает возможность присоединения к растущей грани кристалла отдельных молекул, хотя такой процесс, очевидно, является второстепенным, особенно в случае значительных переохлаждений воды. Рост кристалла может происходить не только в растворе, но и в газовой среде; при этом молекулы воды из пара осаждаются на лед, например в природе образуя снежинки (рис. 3 б).

            В статье [4] приведено выражение Б.В.Дерягина для расчета потока массы растущего льда. Скорость роста кристалла льда определяется скоростью притока вещества или скоростью отвода теплоты кристаллизации. На основе рассмотрения кинетики взаимодействия фаз в области границы фазовых переходов С.Е. Гречищевым получено следующее выражение [2]:

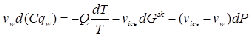
где v_w и v_ice - удельные объемы соответственно пленки воды и льда, q_wпоток влаги, С - коэффициент, G^sk и Р давление соответственно во льду и в водяной пленке. Нетрудно видеть сходство этих двух выражений.

            В последних работах по моделированию кластеры стали описывать как фракталы [4, 5], а кластеризацию рассматривать одним из способов возникновения фракталов в необратимых процессах. Среди таких работ отличается наглядностью модель ограниченной диффузией агрегации (ДОА – так названа в первоисточнике) Сандера для изучения эффектов нелокального поля диффузии [6]. Неупорядоченный, хаотический рост кристалла, отождествляемый с ДОА, доведенной до конечного предела, является следствием движения случайно блуждающих частиц к кластеру, что порождает фрактальные структуры.

            Одним из экспериментальных примеров, подтверждающих адекватность ДОА, является электролитическое осаждение металлов на небольшой электрод. В целях большей наглядности обычно строят сначала двумерную модель кристаллизации вида «частица - кластер», а затем более сложную модель «кластер - кластер» [5]. При этом допускают, что скорость охлаждения достаточно высока, чтобы пренебречь упомянутой растворимостью х' образовавшихся зародышей кристаллов при данной степени их дисперсности. Такое же допущение соблюдают при построении и трехмерной модели, которую уже сравнивают с экспериментами. Моделирование «частица - кластер» на квадратной решетке размером L×L, L=10÷1000 ед., выполняют при соблюдении трех правил: 1) первоначально имеется единственный точечный зародыш, который представляет собой центральную клетку решетки; 2) частица определяется как квадратная клетка с единичной стороной; частица стартует из случайной клетки на краю решетки и совершает случайное блуждание по решетке до тех пор, пока она не соприкоснется одной из частиц кластера или группы соседствующих частиц; 3) процесс прекращается, как только кластер достигает в своем росте края решетки. Правило 1) моделирует рост только одного кластера, 2) - допускает только древовидные кластеры без появления петель, 3) - останавливает численное моделирование.   

   Воспроизведения дендритного роста показано на модели ДОА с одной затравочной частицей в центре квадратной решетки (рис. 3 в) . При этом присоединение частицы может быть слабым — одна-единственная связь с кластером, средним — 2 связи, сильным — 3 связи. Число связей определяют как число вершин частицы, соприкасающиеся с кластером. Легко доказать, что в этой модели число связей не может превышать 3.

            Фрактальную размерность D₀ (ее еще называют клеточной размерностью) множества Х численно определяется следующим. Покроем Х квадратной решеткой, у которой сторона клетки равна ε. Затем подсчитаем число N(ε) клеток, покрывающих Х. Тогда, по определению,

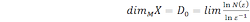
Для двумерного случая фрактальная размерность дендритов близка к 1,7. Это означает, что масса агрегата возрастает как L^1,7, где L — линейный размер, а средняя плотность изменяется как L^1,7/L² = L^-0,3, т.е. убывает, в полном соответствии с внешним видом подобных форм роста. В трехмерной ДОА фрактальная размерность обычно находится вблизи 2,5.

            При ДОА отдельные частицы после некоторых случайных блужданий оседают на агрегате, порождая фракталы, которые моделируют рост ледяных дендритов в воде. Для них характерна древовидная структура с многочисленными «фьордами» на многих размерных масштабах, что также сравнимо с конструкцией снежинки (рис. 3 б, в) с учетом гексагональной тенденции, связанной со строением молекулы воды. Причина образования подобных структур при ДОА заключается в том, что блуждающая частица оседает, как правило, вблизи выступа фрактала, а не в глубине фьорда, как подробнее показано ниже.

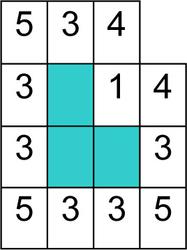
    Для вычисления вероятности прикрепления частицы с кластером заметим, что частица, будучи квадратом, может иметь с кластером одну, две или три общих вершины. На рис. 3 г изображен кластер из трех частиц - клеток, окрашенных в темный цвет. Блуждающая частица может присоединиться к этому кластеру, попав в одну из 12 белых клеток. Число одношаговых путей, по которым частица может попасть в белую клетку, записано внутри клетки. Среди 12 белых клеток имеется 5 угловых, 6 срединных, 1 фьорд.

                 а)                                  

б)                                  

в)                          

г)

Рис. 3. Кристаллические структуры и описывающие их модели: а) микрофотоснимок гексагонального кристалла льда, выросшего из зародыша [2]; б) снежинка под микроскопом [2]; в) кластер в модели ДОА [5]; г) схема кластера из трех частиц с указанием вероятности прикрепления частицы к кластеру [5].

Угловые клетки имеют 1 связь с кластером, срединные — 2 связи, фьорд — 3 связи. Поскольку всего имеется 42 одношаговых маршрута, ведущих в белые клетки извне, то вероятности p_k того, что частица попадет в белую клетку с k связями, равны: p₁=23/42≈0,5476,  p₂ =12/42≈0,4286,  p₃ =1/42≈0,0238.

Видно, что соединиться с кластером внутри фьорда у частицы мало шансов. Это означает, что при реальной кристаллизации внутри фьорда концентрация частиц льда меньше, так как многие из них уже присоединились к кластеру. В окрестности же выступов концентрация высокая, так как пока мало частиц из этой окрестности присоединились к дендриту. Сходство между конструкциями ледяных дендритов и формами ДОА объясняется тем, что оба процесса описываются уравнением Лапласа  из теории потенциала, причем градиент потенциала соответствует полю диффузии в ДОА, а поверхность кластера ДОА — эквипотенциальной поверхности. При таком подходе к ДОА следует, что частицы будут с большей вероятностью прилипать к тем местам кластера, где высок градиент потенциала, т.е. вблизи выступов. «Рост» молнии или ледяного дендрита происходит, как правило, в направлении наибольшего градиента потенциала. Глубокие же фьорды (рис. 3 б, в) хорошо экранированы и поэтому либо растут очень медленно, либо не растут вовсе. Такое соответствие между теорией потенциала и описанным механизмом фрактального роста кристаллов было полностью подтверждено тщательными измерениями и численными решениями потенциального уравнения.

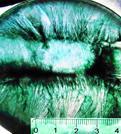
            Формы ледяных кристаллов, нарастающих в растворах на твердом основании, которым в нашем случае является стенка пресс-формы, своеобразны. При толщинах стенок ледяных моделей порядка 10 мм и замораживании в условиях холодильной камеры Nord-155 при указанных выше температурах скорости охлаждения достаточно высоки и дендритная структура, показанная в работе [4] возможна лишь в центре стенки модели в редком случае. Обычно оси кристаллов второго и третьего порядка перестают образовываться и возникают игольчатые (полосчатые) формы (рис. 4а) кристаллов льда, которые нарастают на подложку преимущественно главной осью по нормали к основанию (по так называемому закону Бэртэна [2]) в условиях теплоотдачи в этом направлении, когда переохлаждение в стадию протокристаллизации ограничено более или менее тонким слоем воды, прилегающим к основанию. Чем тоньше переохлажденный слой в момент зарождения кристаллов, тем однообразнее ориентировка. Такое же полосчатое строение кристаллов льда видны в результате кристаллизации из воды с примесями частичек древесного угля, которые располагаются через более или менее равные промежутки в тонких прослойках между плоскостями кристаллов (рис. 4 б).

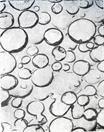
            Если состав ледяной модели вводят растворенные или эмульгированные технологические добавки, например связующего для получения в последующем оболочковой литейной формы путем пропитки контактного слоя песка при таянии этой модели, то характер распределения таких примесей иллюстрирует рис. 4 в, г. На рис. 4в показан лед морской воды [2]. В процессе охлаждения раствора происходит раздельное формирование решеток льда и у каждой из солей. При этом происходит расслаивание раствора - расплава, причем соли вытесняются к периферии области роста зародыша, а затем и кристалла льда. Вокруг кристаллов образуются как бы «клетки» и «каналы» из ячеек раствора повышенной концентрации. Минеральные примеси и растворенные соли в ходе роста распределяются между элементарными пластинками внутри кристаллов и между ними. В соленых льдах рассол образует прослойки в базисных плоскостях кристаллов, разделяющих кристаллы на ряд пластинок. Чем быстрее происходит

а)                               

б)                                     

  в)                       

  г)

 Рис. 4. Ледяные образцы: а, б - моделей толщиной 10 мм, а - лед с добавками чернила, б - с добавками крупинок древесного угля, в - морской лед, г — электоронно-микроскопический снимок скола замороженной эмульсии.  

кристаллизация и чем больше концентрация солей, тем толще прослойки рассола (до нескольких миллиметров при близкой к нулю температуре) и тем тоньше относительно разделяемые ими элементарные пластинки льда. Расстояние между соседними прослойками включений в кристалле тем меньше, чем больше концентрация примесей в растворе.

            На рис. 4в показан электоронно-микроскопический снимок скола замороженной эмульсии типа «вода в масле», образующейся при введении воды в расплав полиуретанового мономера [7]. При таком процессе размер частиц диспергированного полиуретанового латекса составляет 0,03...500 мкм. Достижения в технологии вододисперсионных лаков и смол, основанные на успехах в области эмульсионной полимеризации, а также исследованиях коллоидно-химических свойств полимерных дисперсий и механизма пленкообразования позволили получить ряд новых вододисперсионных связующих материалов, пригодных для замораживания в литейных ледяных моделях. Ученым литейщикам еще предстоит отработать технологии применения этих связующих для получения оболочковых форм вокруг таких моделей, в том числе в паре с быстродействующими отвердителями. Ряд примеров изготовления

а)                                                       

б)                                     

  в)

Рис. 5. Ледяные модели: а, б - модели полумуфт, с открытой пресс-формой (а), с отливкой (б); г – модель шестерни с двумя отливками.

таких ледяных моделей показан на рис. 5, где на первом рис. 5 а показаны ледяные модели (одна с элементами литниковой системы) из технической воды, на рис. 5 б – модель из вышеупомянутого 25%-го раствора жидкого стекла (в сборе с литниковой системой), а также полученная отливка из чугуна СЧ 20; на 5 в - ледяная модель из водного раствора лигносульфонатов технических (ЛСТ) и две отливки из цветных сплавов.

ЛСТ (ГОСТ 13 183–83) являются дешевыми и недефицитными органическими водными связующими, обеспечивающими хорошую выбиваемость форм, в том числе из ХТС. Запланирована отработка технологии получения оболочковых форм, по аналогии с ХТС отверждаемых хромовым ангидридом Сr₂O₃ или другими соединениями с шестивалентным хромом в количестве 0,3-0,7% от массы смеси. ЛСТ применяют в формовочных смесях в количестве 3–5% (реже до 8%),  в сочетании с глиной 2–3%, или природными формовочными глинистыми песками. При введении ЛСТ в модельную композицию ее разбавляют водой до плотности не выше 1,17-1,20 г/см³, температуру модели понижают до –(17-20) °С, а порошкообразный отвердитель помещают в облицовочный песчаный слой.

При введении в материал ледяных моделей органических связующих уместно учитывать возможность проявления механизма действия биологических криопротекторов. В медицинской и лабораторной практике используют около десятка таких соединений, действующих аналогично белкам, предотвращающим кристаллизацию льда в клеточном растворе. Считается, что они адсорбируются на поверхности ледяного кристалла и тем самым препятствуют его росту, что наблюдается на полученных нами образцах с декстрином в виде мелкозернистой структуры, а на некоторых образцах, полученных в одинаковых условиях с образцом (рис. 4а, зерна видны невооруженным глазом), сетка межзерновых границ была столь мелкой, что без увеличения не просматривалась.

В статье рассмотрен комплекс вопросов, касающихся механизма и кинетики затвердевания льда при получении одноразовой литейной модели, распределение во льде примесей. На примере исследования этого процесса показано применение современных математических методов наглядного моделирования кристаллизации с учетом теории кластеров и фракталов, приведены примеры литейных моделей и их структур. Физическая составляющая моделирования стремится в предметной области ответить на исследовательский вопрос, как происходит рост ледяных образований во время формирования модели, математическая составляющая дает возможность построить и изучить численную модель, дающую представление о механизмах и причинах роста кристаллов. С дидактической точки зрения для технологического использования важны аспекты адекватной интерпретации достигнутых результатов в терминах физической модели, некоторые полученные численные характеристики, а также предложенные направления исследований по доведению технологии ЛЛМ до опытного, а затем промышленного применения.

Литература

1. Дорошенко В. С. Предпосылки создания технологии литья по ледяным моделям в вакуумируемых формах // Металл и литье Украины. –  2009. - № 4-5. – С. 18 – 23.

2. Хименков А. Н., Брушков А. В. Ведение в структурную криологию. М.: Наука.2006. 279 с.

3. Цытович Н.А. Механика мерзлых грунтов. М.: Высшая школа. – 1973. – C. 28 – 32.

4. Дорошенко В. С., Кравченко В. П. Структура литейной ледяной модели с точки зрения теории фракталов // Металл и литье Украины. – 2010.№ 3 . – С. 33-37.

5. Осташков В.Н., Скоробогатов Н. В. Наглядное моделирование дендритных структур // Нефтегазовое дело. – 2006. С. 7 – 13.

6. Сандер Л. Континуальная ДОА: случайный фрактальный рост, порождаемый детерминистической моделью / Фракталы в физике. Труды VI международного симпозиума по фракталам в физике (МЦТФ, Триест, Италия, 9 – 12 июля 1985). — М.: Мир, 1988.— С. 336 – 344.

7. Толмачев И. А., Верхоланцев В.В. Новые вододисперсионные краски. -Л.: Химия, 1979.С. 142.