J. Chem. Sci., Vol. 121, No. 5, September 2009, pp. 839–848. © Indian Academy of Sciences.
839
Dedicated to the memory of the late Professor S K Rangarajan
Structure and stability of spiro-cyclic water clusters
Chemical Laboratory, Central Leather Research Institute, Council of Scientific and Industrial Research,
Adyar, Chennai 600 020
Indian Institute of Science Education and Research (IISER), Mohali, Sector 26, Chandigarh 160 019
Honorary Professor, Jawaharlal Nehru Centre for Advanced Scientific Research, Bangalore 560 064
e-mail: subuchem@hotmail.com; nsath@iitk.ac.in
Структура и стабильность спирально-циклических кластеров воды
Abstract. The structure and stability of spiro-cyclic water clusters containing up to 32 water molecules
have been investigated at different levels of theory. Although there exist minima lower in energy than
these spiro-cyclic clusters, calculations at the Hartree–Fock level, density functional theory using B3LYP
parametrization and second order Møller–Plesset perturbation theory using 6-31G and 6-311++G
basis sets show that they are stable in their own right. Vibrational frequency calculations and atoms-in
molecules analysis of the electron density map confirm the robustness of these hydrogen bonded clusters.
Keywords. Hydrogen bonding; water clusters; spiro-cyclic; atoms-in-molecules.
1. Introduction
H-bonding in water clusters has been the subject of
several experimental and theoretical investigations
due to its importance in various real life systems.
High level ab initio calculations predict the structure
and stability of small water clusters with near quan
titative accuracy.
These studies have been found to
be extremely useful in interpreting the high-resolu
tion spectral data obtained from size and mass selec
tive beam techniques.
These calculations
provide valuable information on H-bonding and also
take us beyond what is easily obtained experimen
tally. The 12-mer, 16-mer and 20-mer of the water
molecule seem to prefer stacked cube and stacked
pentagonal geometries.
The much anticipated
buckyball structure is not the most stable geometry
for the water 20-mer!
It is well-known from the crystal structure data
base that the water molecule plays different roles in
the stabilization of crystal structures and displays a
variety of structural topologies in crystal structures
and in confined environments.
The surge in activity in the area of supramolecular chemistry ex
emplifies the importance of water mediated crystalli
zation and H-bonding interaction.
Most of the structural arrangements and shapes
exhibited by water clusters in various environments
are already known in organic chemistry. For exam
ple, water hexamer exists in boat and chair forms
and these structural motifs are known for cyclohex
ane. Similarly, water octamer assumes the shape of a
cubane. In all these organic moieties, every carbon
atom is invariably sp
hybridized and forms a maxi
mum of four covalent bonds in a tetrahedral fashion.
The oxygen atom in water also exhibits ~sp
hybridization and can form a maximum of four hydrogen
bonds as illustrated in scheme 1. In classical organic
chemistry, spiro-cyclic molecules are also interest
ing from structure and reactivity point of view.
Hence, it is interesting to probe the possibility of the
existence of analogous spiro-cyclic motifs in water
clusters. In the present study, the structure and sta
bility of spiro-cyclic water clusters have been inves
tigated and compared with the most stable water
clusters using ab initio and density functional theo
retic methods.
2. Computational details
Geometries of all the water clusters under investiga
tion have been optimized without any constraint at
different levels of theory using the G98W suite of
programs.
Stabilization energies (SEs) of all the
clusters have been calculated using the supermo
lecule approach and corrected for basis set superpo
sition error (BSSE) following the procedure adopted
by Boys and Bernardi:
where Ecluster is the energy of the cluster, n the total
number of molecules in the cluster and Ei the energy
of the ith monomer in its specific location computed
using the basis set for the n-mer. The relative popu
lation of various conformers for each (H2O)n cluster
as a function of temperature is computed using the
Boltzmann distribution formula:

where kB is the Boltzmann constant, En is the rela
tive energy of the conformer with respect to the
most stable geometry and T is the temperature. To
ensure that the optimized geometries obtained corre
spond to true minima in the energy space, vibra
tional frequencies were calculated at HF/6-31G and
HF/6-311++G levels. They were scaled by a fac
tor of 0 8929 and 0 9070, respectively. The theory of
atoms-in-molecules (AIM)
was used to character
ize the hydrogen-bonding interaction using the topo
logical properties of the electron density at the
hydrogen bond critical point (HBCP) using the
AIM2000 package.
3. Results and discussion
3.1 Geometries
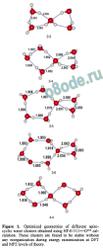
this study are represented schematically in scheme 1.
The size of the rings formed in each cluster is used
in the nomenclature. For example, the cluster 3–3
has two trimer rings arranged in a spiro-cyclic fash
ion. The optimized geometries of different spiro
cyclic water clusters are shown in figures 1 and 2.
Of all the water clusters considered, 3–3, 3–4, 3–5,
3–6 and 4–4 retain their spiro-cyclic structures at all
levels of calculation. However the clusters, 4-5, 4-6,
5-5, 5-6 and 6-6 rearrange from the initial spiro
cyclic structure during optimization. The increase in
the cluster size in each ring decreases the donor–
acceptor interaction between the nearby water mole
cules and as a consequence the spiro-cyclic structure
collapses.
In all the spiro-cyclic water clusters, the central
water molecule, which is shared by both the rings, is
tetra-coordinated. In this mode of interaction, the
central water molecule accepts two protons and also
donates two protons, resulting in an overall stabili
zation of the spiro-cyclic structure. A close scrutiny
Figure 1. Optimized geometries of different spiro
cyclic water clusters obtained using HF/6-311++G cal
culation. These clusters are found to be stable without
any reorganization during energy minimization at DFT
and MP2 levels of theory.
Scheme 1. Schematic representation of spirocyclic models (organic and water
cluster) considered in this study.
of the structures reveals that the two rings are or
thogonal to each other, similar to their organic
counter parts. A comparison of the geometries ob
tained from ab initio calculations for 3–6, 4–6, 5–6
and 6–6 clusters shows that the hexamer ring adopts
a chair form in all the cases. The pentamer ring
found in 3–5, 4–5, 5–5 and 6–5 clusters deviates
slightly from the planar arrangement. The trimer and
tetramer rings are planar as observed in the most
stable water clusters. Some of these clusters are not
stable at higher level calculations. However, these
spiro-cyclic structures (for example 6–6 and 4–4)
are observed in certain crystals
suggesting that
the stabilization of these structural motifs must be
arising from additional interaction with the host
molecules and crystal packing. In contrast, the 3–3,
3–4, 3–5, 3–6 and 4–4 spiro clusters seem to be sta
ble even in the absence of any host lattice and asso
ciated packing effect.
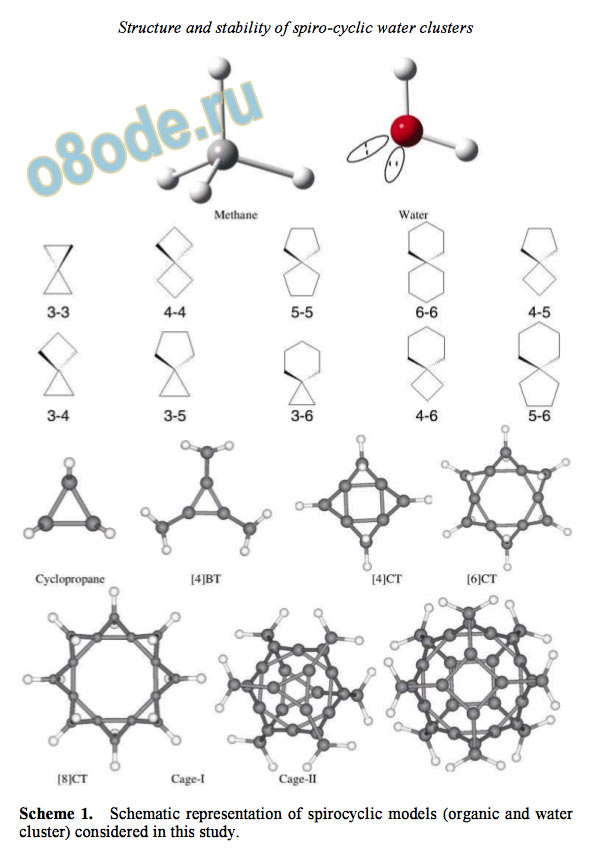
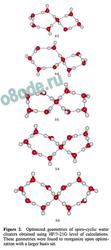
spiro-cyclic structures reveals several exotic spiro
cyclic and spiro-annulated structures.
Some of
the spiro-cyclic and spiro-annulated water clusters
optimized at the HF/6-311++G level of theory are
shown in figure 3. The possibility of forming such
structures in the absence of a host or a crystal pack
ing environment has been examined. The spiro
annulated structures are classified as unbranched
(U), branched (B) and cyclic (C). The total number
of trimer rings present in each cluster is denoted as
[n]. For example, the cluster [4] is a spiro-annulated
water cluster with four trimer rings.
Figure 2. Optimized geometries of spiro-cyclic water
clusters obtained using HF/3-21G level of calculations.
These geometries were found to reorganize upon optimi
zation with a larger basis set.
In this investigation, one B, four C and two caged
spiro-annulated clusters have been studied. In gen
eral, all the C structures have an even number of
spiro-annulated trimer rings ([n]) with a planar cen
tral ring. Any two adjacent trimer rings are arranged
in an up and down fashion with respect to the central
planar ring and hence (n/2) trimer rings are above
and (n/2) trimer rings are below the central plane.
Along with these structures, two cage structures
consisting of only spiro-annulated trimer rings have
been studied. These rings are interconnected in a
beautiful manner that results in a regular cage struc
ture. It is important to note that in all these clusters,
the basic spiro-cyclic 3–3 cluster is observed with
out any structural deformation. In addition, these
clusters are stable without any host and packing
environment. All the spiro-annulated structures are
similar in shape to that of the corresponding organic
molecules as illustrated in scheme 1.
3.2 Energetics
Stabilization energies (SEs) obtained from HF cal
culations using the 6-31G and 6-311++G basis
sets are listed in table 1 for different water clusters.
SEs obtained from MP2/6-311++G and
DFT(B3LYP)/6-311++G calculations are listed in
table 2. The SEs obtained from HF/6-31G and
HF/6-311++G levels of calculation are corrected
for zero point energy (ZPE). For all other calcula
tions, only BSSE corrections are included. As was
expected, there is a decrease in the SE with an
increase in the size of the basis set. Further, the SEs
obtained from HF, DFT(B3LYP) and MP2 levels of
theory using the 6-311++G basis set follow the
order HF < DFT(B3LYP) < MP2.
The SEs obtained from DFT(B3LYP)/6-311++G
calculations for the spiro-cyclic water clusters are
compared with those of the most stable water clus
ters in figures 4a and b. Clearly, the spiro-cyclic wa
ter clusters are less stable than the most stable water
clusters. The SE of the 3–3 cluster (with five water
molecules), for example, is lower in energy than the
most stable (cyclic) pentamer by 9 2 kcal/mol,
despite the fact that the former has an additional
hydrogen bond over the latter. The SE of the 3–4
cluster (six water molecules) is less than that of the
most stable (cage) hexamer by 6 1 kcal/mol. The
clusters 4–4 and 3–5 have seven water molecules
each. However, the SE of the 4–4 cluster is larger
than that of 3–5 by 1 9 kcal/mol and less than that of
Structure and stability of spiro-cyclic water clusters
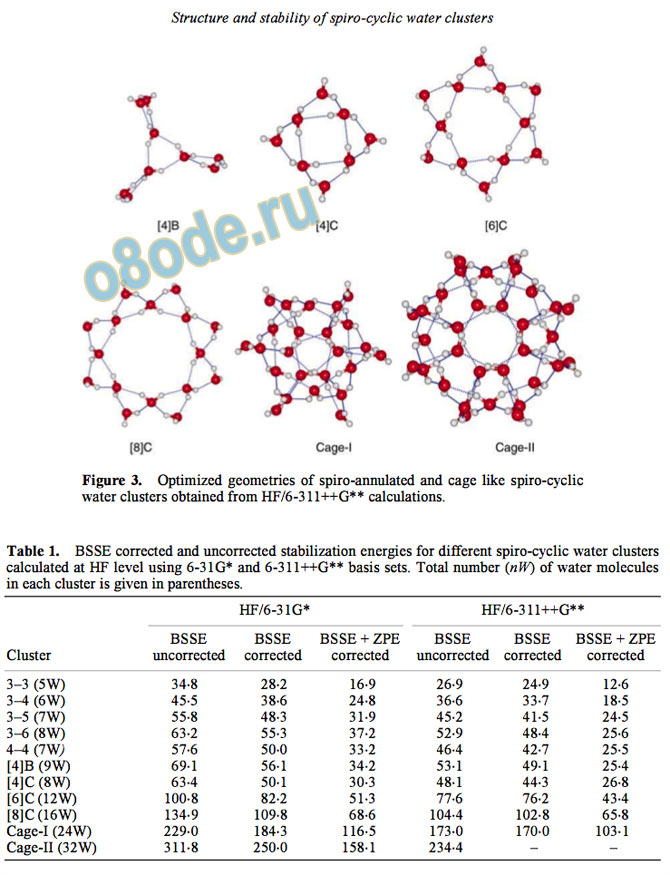
Figure 3. Optimized geometries of spiro-annulated and cage like spiro-cyclic
water clusters obtained from HF/6-311++G calculations.
Table 1. BSSE corrected and uncorrected stabilization energies for different spiro-cyclic water clusters
calculated at HF level using 6-31G and 6-311++G basis sets. Total number (nW) of water molecules
in each cluster is given in parentheses.
the most stable heptamer by 6 2 kcal/mol. To gain
further insight into the energetics of various spiro
cyclic clusters, the SE per H-bond has been calcu
lated. It is evident from the results presented in
figure 4b that the SE per H-bond for 3–3 cluster is
less than that of the corresponding most stable cyclic
pentamer. However, for other spiro-cyclic water
clusters such as 3–4, 3–5, 3–6 and 4–4, the SE per
H-bond is larger than that of the corresponding most
stable water clusters. The difference falls in the
range 0 5–1 2 kcal/mol.
It is important to note from the SE values of vari
ous spiro-cyclic clusters that as the size of the spiro
cyclic water cluster increases, the difference bet-
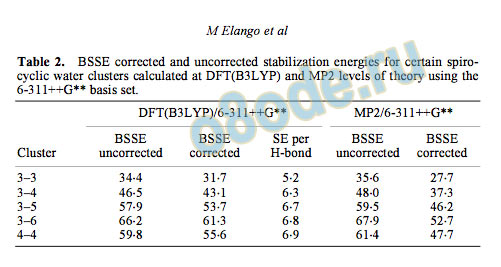
Table 2. BSSE corrected and uncorrected stabilization energies for certain spiro
cyclic water clusters calculated at DFT(B3LYP) and MP2 levels of theory using the
6-311++G basis set.
(b) stabilization energy per H-bond of the most stable
water cluster and the corresponding spiro-cyclic water
cluster containing the same number of water molecules
calculated at DFT(B3LYP)/6-311++G level of theory.
The differences in energies in kcal/mol units are included
in the figure.
ween the SE of spiro-cyclic and the most stable
water cluster also increases. This is partly because
the number of unused potential hydrogen bonding
interaction sites is more in spiro-cyclic water clus
ters than in the most stable water clusters. These
sites would clearly contribute to hydrogen bond
formation with the host molecules and hence
the stability of spiro-cyclic clusters in organic and
inorganic host lattices.
In addition to the spiro-cyclic water clusters, the
SE of hitherto unreported cage-I and cage-II struc
tures are also listed in table 1. These cages consist of
24 and 32 water molecules, respectively. Their SEs
with BSSE corrections are 184 and 250 kcal/mol,
respectively, at the HF/6-31G level of calculation.
The respective SE per H-bond for these clusters is
4 5 and 3 4 kcal/mol.
The population of various conformers for differ
ent water clusters [(H2O)n, where n = 5, 6, 7, 8] as a
function of temperature is illustrated in figure 5. It is
evident from the figure that as the number of
conformers increases for any particular (H2O)n, the
contribution by the spiro-cyclic water clusters also
increases. When compared to the most stable
conformation, the population is low for all other
conformers investigated.
3.3 Atoms-in-molecules
The AIM theory has been used to characterize the
hydrogen bonding interaction in spiro-cyclic water
clusters and the resulting parameters are listed in
table 3. Figure 6 gives the AIM topology for all the
spiro-cyclic water clusters. The electron density ( )
values at the HBCPs are ~10
indicating non
covalent interaction.
The values of the Laplacian of
electron density at the HBCPs are all positive, a
Structure and stability of spiro-cyclic water clusters
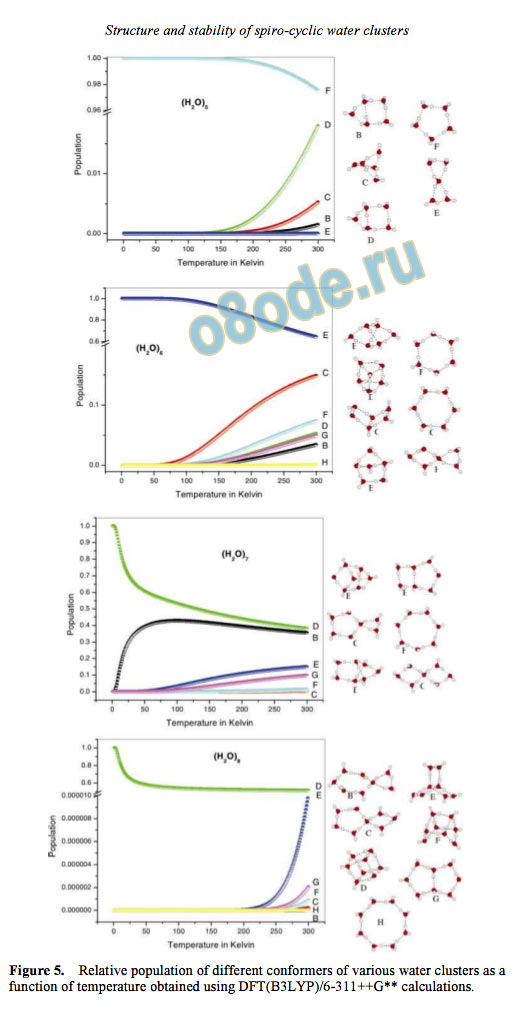
Figure 5. Relative population of different conformers of various water clusters as a
function of temperature obtained using DFT(B3LYP)/6-311++G calculations.
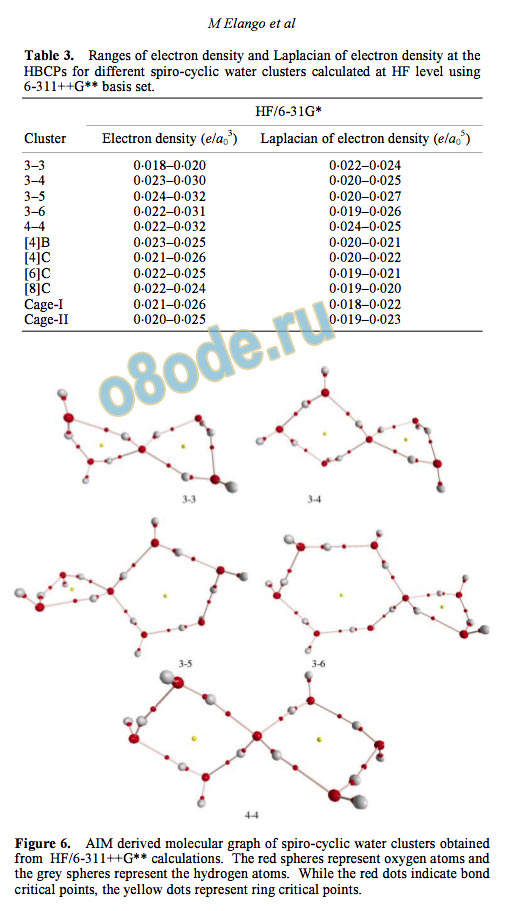
Table 3. Ranges of electron density and Laplacian of electron density at the
HBCPs for different spiro-cyclic water clusters calculated at HF level using
6-311++G basis set.
Figure 6. AIM derived molecular graph of spiro-cyclic water clusters obtained
from HF/6-311++G calculations. The red spheres represent oxygen atoms and
the grey spheres represent the hydrogen atoms. While the red dots indicate bond
critical points, the yellow dots represent ring critical points.
The
molecular graphs show rich electron density topo
logical features in spiro-cyclic clusters and the pre
sence of the ring structure is confirmed by the
presence of ring critical points. The molecular
graphs further confirm that there is no other short
contact or non-bonded interaction between the spiro
cyclic rings.
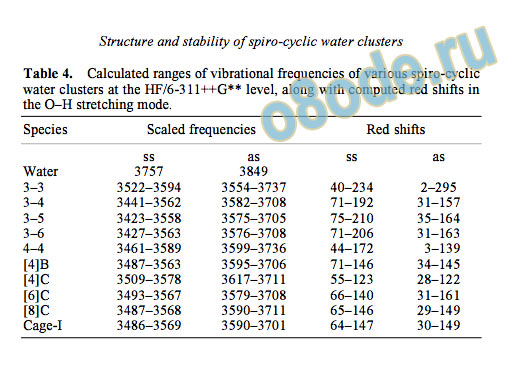
Table 4. Calculated ranges of vibrational frequencies of various spiro-cyclic
water clusters at the HF/6-311++G level, along with computed red shifts in
the O–H stretching mode.
Species Scaled frequencies Red shifts
3.4 Vibrational frequencies
Symmetric and asymmetric O-H stretching frequen
cies for a water molecule and spiro-cyclic and spiro
annulated water clusters as computed by the HF/6
311++G method and scaled by a factor of 0 9070
are reported in table 4. The calculated red shifts fall
in the range 40–234 cm
–1
for symmetric stretching
and 3–295 cm
–1
for asymmetric stretching. This
again is characteristic of hydrogen bonded systems.
4. Conclusions
Hartree–Fock, density functional and second order
Møller–Plesset perturbation theoretic calculations
using reasonably large basis sets show that several
spiro-cyclic clusters are stable in their own right.
Frequency calculations and atoms-in-molecules
analysis of the electron density topology of these
clusters reveal the hydrogen bonding in these clus
ters and their robustness. While they may not be
common in gas phase, they are stable enough and
they have enough potential hydrogen bonding sites
that they can be formed in host lattices and in crystal
packing environments.
Acknowledgements
This study was supported in part by a grant from the
Council of Scientific and Industrial Research
(CSIR), New Delhi. ME thanks the CSIR for a Senior
Research Fellowship. NS thanks the Department of
Science and Technology (DST), New Delhi for a J C
Bose Fellowship.
References
1.
Pauling L 1960 The nature of the chemical bond
(Cornell University Press)
2.
Jeffrey G A 1997 An introduction to hydrogen bond
ing (Oxford University Press)
3.
Scheiner S 1997 Hydrogen bonding. A theoretical
perspective (Oxford University Press)
4.
Desiraju G R and Steiner T 1999 The weak hydrogen
bond: In structural chemistry and biology (Oxford
University Press)
5.
Steiner T 2002 Angew. Chem. Int. Ed. 41 48
6.
Desiraju G R 2002 Acc. Chem. Res. 35 565
7.
Saenger W 1984 Principles of nucleic acid structure
(Springer-Verlag)
8.
Schulz G E and Schirmer R H 1979 Principles of
protein structure (Springer-Verlag)
9.
Maheshwary S, Patel N, Sathyamurthy N, Kulkarni A
D and Gadre S R 2001 J. Phys. Chem. A105 10525
10.
Wales D J and Hodges M P 1998 Chem. Phys. Lett.
286 65
11.
Wernet Ph, Nordlund D, Bergmann U, Cavalleri M,
Odelius M, Ogasawara H, Naslund L-Å, Hirsch T K,
Ojamae L, Glatzel P, Pettersson L G M and Nilsson
A 2004 Science 304 995
12.
James T, Wales D J and Hernández-Rojas J 2005
Chem. Phys. Lett. 415 302
13.
Kim J and Kim K S 1998 J. Chem. Phys. 109 5886
14.
Buck U, Ettischer I, Melzer M, Buch V and Sadlej J
1998 Phys. Rev. Lett. 80 2578
15.
Harvey J N, Jung J O and Gerber R B 1998 J. Chem.
Phys. 109 8747
16.
Kim J, Mujumdar D, Lee H M and Kim K S 1999 J.
Chem. Phys. 110 9128
17.
Brudermann J, Melzer M, Buck U, Kazimirski J K,
Sadlej J and Buch V 1999 J. Chem. Phys. 110 10649
18.
Hodges M and Wales D J 2000 Chem. Phys. Lett. 324
279
19.
Chaban G M, Xantheas S S and Gerber R B 2003 J.
Phys. Chem. A107 4952
M Elango et al
848
20.
Myshakin E M, Diri K and Jordan K D 2004 J. Phys.
Chem. A108 6752
21.
Tachikawa H 2004 J. Phys. Chem. A108 7853
22.
Choi Y C, Pak C and Kim K S 2006 J. Chem. Phys.
124 094308
23.
Ludwig R 2007 Chem. Phys. Chem. 8 938
24.
Matsumoto Y, Ebata T and Mikami N 2000 J. Mol.
Struct. 552 257
25.
Guchhait N, Ebata T and Mikami N 2000 J. Phys.
Chem. A104 11891
26.
Fujii A, Patwari G N, Ebata T and Mikami N 2002
Int. J. Mass Spectrom. 220 289
27.
Miyazaki M, Fujii A, Ebata T and Mikami N 2004
Science 304 1134
28.
Steinbach C, Andersson P, Kazimirski J K, Buck U,
Buch V and Beu T A 2004 J. Phys. Chem. A108
6165
29.
Steinbach C, Andersson P, Melzer M, Kazimirski J
K, Buck U and Buch V 2004 Phys. Chem. Chem.
Phys. 6 3320
30.
Gruenloh C J, Hagemeister F C and Zwier T S 2000
Recent theoretical and experimental advances in
hydrogen-bonded clusters (Kluwer) pp. 83–99
31.
Zwier T S 2001 J. Phys. Chem. A105 8827
32.
Zwier T S 2004 Science 304 1119
33.
Liu K, Cruzan J D and Saykally R J 1996 Science
271 929
34.
Ludwig R 2001 Angew. Chem. Int. Ed. 40 1808
35.
Atwood J L, Barbour L J, Ness T J, Raston C L and
Raston P L 2001 J. Am. Chem. Soc. 123 7192
36.
Moorthy J N, Natarajan R and Venugopalan P 2002
Angew. Chem. Int. Ed. 41 3417
37.
Ghosh S K and Bharadwaj P K 2003 Inorg. Chem. 42
8250
38.
Ghosh S K and Bharadwaj P K 2004 Angew. Chem.
Int. Ed. 116 4490
39.
Ghosh S K and Bharadwaj P K 2004 Inorg. Chem. 43
3771
40.
Saha B K and Nangia A 2005 Chem. Commun. 24
3024
41.
Mukherjee A, Saha M K, Nethaji M and Chakravarty
A R 2004 Chem. Commun. 21 716
42.
Nangia A 2007 Encyclopedia of supramolecular
chemistry (eds) J L Atwood and J W Steed (Taylor &
Francis) pp. 1–9
43.
Meijere A D, Kozhushkov S I and Schill H 2006
Chem. Rev. 106 4926
44.
Frisch M J, Trucks G W, Schlegel H B, Scuseria G E,
Robb M A, Cheeseman J R, Montgomery J A Jr, Vre
ven T, Kudin K N, Burant J C, Millam J M, Iyengar S
S, Tomasi J, Barone V, Mennucci B, Cossi M, Scal
mani G, Rega N, Petersson G A, Nakatsuji H, Hada
M, Ehara M, Toyota K, Fukuda R, Hasegawa J,
Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H,
Klene M, Li X, Knox J E, Hratchian H P, Cross J B,
Bakken V, Adamo C, Jaramillo J, Gomperts R,
Stratmann R E, Yazyev O, Austin A J, Cammi R,
Pomelli C, Ochterski J W, Ayala P Y, Morokuma K,
Voth G A, Salvador P, Dannenberg J J, Zakrzewski V
G, Dapprich S, Daniels A D, Strain M C, Farkas O,
Malick D K, Rabuck A D, Raghavachari K, Fores
man J B, Ortiz J V, Cui Q, Baboul A G, Clifford S,
Cioslowski J, Stefanov B B, Liu G, Liashenko A,
Piskorz P, Komaromi I, Martin R L, Fox D J, Keith
T, Al-Laham M A, Peng C Y, Nanayakkara A, Chal
lacombe M, Gill P M W, Johnson B, Chen W, Wong
M W, Gonzalez C and Pople J A 1998 Gaussian 03,
Revision E.01, Gaussian, Inc., Pittsburgh, PA
45.
Boys S F and Bernardi F 1970 Mol. Phys. 19 553
46.
Bader R F W 1990 Atoms in molecules: a quantum
theory (Clarendon Press)
47.
AIM 2000 Biegler-Konig F, Schonbohm J, Derdau R,
Bayles D and Bader R F W 2000 Version 1
(Bielefeld, Germany)
48.
Garc a R L, Murillo B M D, Barba V, Hopfl H,
Beltran H I and Rivera L S Z 2005 Chem. Commun.
22 5527
49.
Choudhury S R, Jana A D, Colacio E, Lee H M,
Mostafa G and Mukhopadhyay S 2007 Crystal
Growth & Design 7 212
50.
Maciel G S, Bitencourt A C P, Ragni M and Aqui
lanti V 2007 Int. J. Quantum Chem. 107 2697
51.
Parthasarathi R, Subramanian V and Sathyamurthy N
2006 J. Phys. Chem. A110 3349