John von Neumann Institute for Computing
Cooperativity in Large Water Clusters Liquid Water, Iceand Clathrates
RogerA. Klein publishedin NICSymposium2006, G.M unster,D.Wolf,M.Kremer(Editors), Johnvon Neumann Institute for Computing, Julich, NIC Series, Vol. 32,ISBN3-00-017351-X,pp. 65-74,2006. 2006 by Johnvon Neumann Institutefor Computing
Permission to make digital or hardcopies of portions of this work for personal or classroomuseisgrantedprovidedthat thecopiesarenot madeor distributedfor pro t or commercial advantageandthat copies bear thisnoticeandthefull citationonthe rst page. Tocopyotherwise requirespriorspeci cpermission by the publishermentionedabove. www.fz-juelich.de/nic-series/volume32 Cooperativity in Large Water Clusters Liquid Water, Ice and Clathrates Roger A. Klein Institute for Physiological Chemistry University of Bonn, Nussallee 11, 53115 Bonn, Germany E-mail: klein@institut.physiochem.uni-bonn.de
Кооперация больших водяных кластеров воды, льда и клатратов

Long-range order in the form of water clusters is what gives liquid water, ice and gas clathrates their particular properties. Liquid water, made up of hydrogen-bonded, cross-linked H2O molecules, should boil nearly 200oC lower at approximately -100oC instead of at +100oC, based on its position as a Group VIA hydride together with H2S, H2Se and H2Te. The presence of cooperative hydrogen bonding between the water monomers gives rise to liquid and solid phases with considerable long-range order which helps to explain many of their physical properties. Liquid water is thought to be composed of ’ ickering’ clusters of hexagonally coordinated molecules in which the O-H bonds and the two lone-pair electrons of the oxygen atom are arranged in a tetrahedrally symmetric fashion. Thus each water molecule in liquid water, and indeed in Ice Ih, is bound on average by four hydrogen bonds to neighbouring water molecules as a double hydrogen bond donor / double hydrogen bond acceptor. Because the O-HD...OA-H hydrogen bonds form extended networks of alternating donors and acceptors there is considerable cooperativity which enhances the stability of these networks and is the explanation for the unusual properties of water, such as its speci c heat or boiling point.
All the ice polymorphs consist of variations on the theme of tetracoordinated water molecules in the form of hexagons. On the other hand, the gas clathrates are composed of tetracoordinated water molecules hydrogen bonded to give structures formed of edge-sharing pentagons which are stable under moderate pressures and reduced temperatures, such as are found on the ocean oor. Deep-sea methane clathrates, produced naturally, are arguably the largest renewable energy resource available if methods for the recovery of the methane gas without disturbing the equilibtrium of the oceans could be developed.
This project is centred on understanding the electronic and quantum chemical interactions which stabilise these hydrogen-bonded water clusters with hexagonal (water and ice) or pentagonal (clathrates) motifs and which give rise to their particular physicochemical properties. Because it is necessary to study water clusters as large as (H2O)24 at a high level of quantum chemical theory, it is essential to use computational facilities such as those available on the IBMSC-Jump machine at NIC in J ulich.
1 Introduction
Accurate electronic models of the molecular structure of liquid water are necessary not only in order to understand the behaviour of water itself but are also particularly important for the modelling of biologically signi cant molecules such as proteins or nucleic acids which are hydrated in aqueous solution, being surrounded by a structured solvation shell of water molecules.
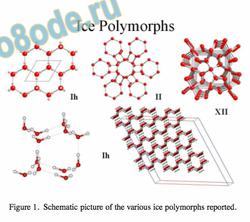
The methane clathrates, which are found in the deep oceans1 , represent a large, potentially usable renewable energy resource as the methane is produced by radioactive decay from the earth’s core2 . Clathrates are, however, unstable at ambient temperatures and
Figure 1. Schematic picture of the various ice polymorphs reported.
pressures so that an understanding of the physical chemistry of these supramolecular aggregates is required in order to able to extract them without disturbing the environmental equilibrium. Explosive de-gassing of a large body of methane clathrates would lead potentially to an environmental disaster as methane CH4 is a highly effective ’greenhouse’ gas. Methane clathrate under high pressure is also thought to be the source of the methane in Titan’s atmosphere3.
Whether one is dealing with liquid water, ice or gas clathrates, cooperative effects between hydrogen-bonded water molecules are highly important in determining physical behaviour as well as the electronic properties of these supramolecular aggregates.
2 Background
Liquid water is thought of in terms of so-called ’ ickering clusters’ of hexagonal, interlocked ring systems made up of six hydrogen-bonded water molecules4. This produces some long-range order even in liquid water at ambient temperatures, extending on average out to at least the second or third hydration shell, as evidenced by radial distribution functions determined from X-ray or neutron scattering experiments5, 6.
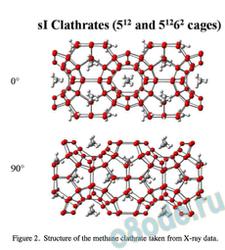
On the other hand, gas clathrates are made up of edge-fused pentagonal arrays of water molecules7, 8, hydrogen bonded to one another so that there is a repetitive donor-acceptor pattern. The structure for the sI methane clathrate in shown in Fig. 2 with two views at right angles to one another.
Figure 2. Structure of the methane clathrate taken from X-ray data.
3 Cooperativity
Cooperativity may be de ned as occurring when the total effect, for example, stabilisation energy, exceeds the simple, additive sum of the individual, isolated effects, e.g., the interaction energy between two water molecules in the water dimer, making up the total. The term cooperativity may also be applied to hydrogen bonding in water clusters, in which the electron density and its Laplacian at the bond critical point (BCP) for each hydrogen bond are greater than those observed for the water dimer.
Cooperativity may be thought of as synonymous with synergism. This is most clearly seen in the physical synchronisation, or phase-locking, of the O–H vibrational stretching modes in the calculated IR spectrum for water clusters. Cooperativity or synergism are also responsible for the very large OH-stretch IR red-shifts, of the order of 500–600 cm-1, observed for large water clusters both experimentally and theoretically. The physical basis for this cooperativity expressed as synchronisation of the O–H stretching vibrations in liquid water, lies in ultrafast relaxation (approx. 4 pS), a short F orster radius and consequently highly ef cient resonant intermolecular transfer of vibrational energy9, 10.
3.1 Electron Density Topology
An analysis of the electron density topology for a relatively weak interaction such as a hydrogen bond can provide extensive information on the type of bonding present. The electron density distribution is obtained by generating a wave function le in Cartesians, followed by an analysis of the shape of the three-dimensional electron density surface, i.e., its topology. Four types of non-degenerate Morse critical points can be distinguished.
All critical points are charactersised by a rank and signature. A bond critical point (BCP) has a rank of 3 and a signature of -1, abbreviated to (3,-1), meaning that the surface is three-dimensional and that there are two negative curvatures and one positive curvature at critical point. A BCP represents an electron density minimum along the axis joining the nuclear attractors, and a maximum in the plane orthogonal to this line. Other critical points are associated with rings (3,+1), cages (3,+3) and nuclei (3,-3). Bader has proposed an electron density partitioning system involving the zeroux condition which he has incorporated into his ’Atoms in Molecules’ theory - the so-called AIM theory11. This partitioning scheme has the advantage that it is mathematically and quantum mechanically more rigorous than other methods for partitioning electron density space. The value of the electron density and its Laplacian (equation 1) at the BCP enables a distinction to be made between a ’shared’ interaction – typical for a covalent bond – and a ’closed shell’ interaction - characteristic of weaker interactions such as hydrogen bonding, electrostatic and van der Waals type interactions. A negative Laplacian indicates a relative excess of charge at the BCP, characteristic of covalent bonding or a shared interaction, and a positive value the reverse, typical of a closed–shell interaction.
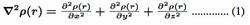
Cooperativity is manifest by shortening of the H...O hydrogen bond donor-acceptor distance and by an increase in the electron density at the (3,-1) bond critical point (BCP), as shown in Fig. 3 and Fig. 4, as well as in the Laplacian of rho, Natural bond orbital (NBO) analysis12 shows increasing orbital overlap for the oxygen lone-pair bonding orbital and the O–H antibonding orbital, no = ⇒ [O-H] , with increasing electron occupancy in the [O-H] antibonding orbital and enhanced second-order perturbation or Fock matrix element deletion stabilisation energies, as well as increasing %s character of the lone pair electrons.
At an atomic level, increasingly cooperative hydrogen bonding in large water clusters is associated with an increased negative charge (electrostatic monopole moment) on the oxygen acceptor atom, stabilisation of the oxygen atom, with decreased charge (increased positive charge) on the hydrogen donor atom, destabilisation of the hydrogen, and a marked decrease in both atomic dipole polarisation and atomic volume for the hydrogen atom. Increased polarisation of the donor and acceptor in terms of charge, ... +, corresponds with the classical Pauling view of hydrogen bonding. Wave function contraction for the hydrogen atom, i.e., a reduction in atomic volume, is very marked as the strength of hydrogen bonding increases. From a non-bonded value of around 21-22 au for the hydrogen atom (3.11-3.26 A3 , equivalent to an atomic radius of approx. 0.91-0.92 A), values of 8-9 au are typical for strongly cooperative environments in tetrahedrally symmetric water clusters. In other highly symmetric, strongly hydrogen bonded structures such as protonated hydrated carbonyl compounds, atomic volume for the hydrogen atom is further reduced to as low as 6 au (0.6 A3 ), with atomic dipole polarisation being close to zero.
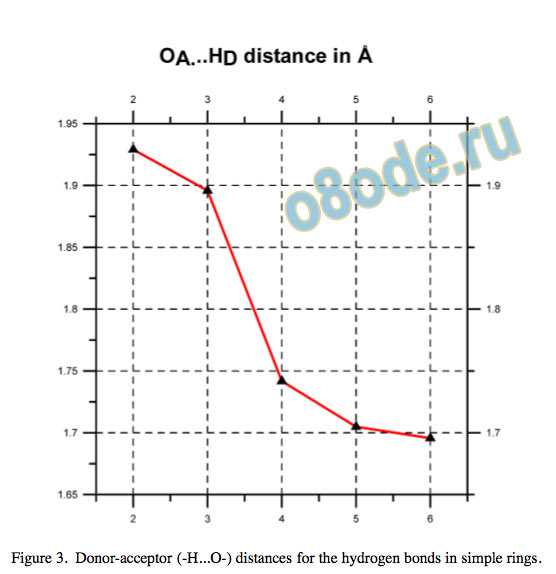
Increasing cooperativity is more associated with a greater degree of tetrahedral symmetry in water clusters, together with occupation of both pairs of H-donor and lone-pair acceptor sites, than with cluster size alone, once an optimal ring size of ve or six water molecules has been reached. Thus it is no accident that the hexagonal motif in liquid water and ice, or the edge-fused pentagonal motif in the gas clathrates, both represent a structural element for bi-coordinated water molecules in which cooperativity is maximised. Although
Figure 3. Donor-acceptor (-H...O-) distances for the hydrogen bonds in simple rings.
further coordination of the water molecules ultimately giving almost perfect tetrahedrally symmetrically 4-coordinated waters in the cluster, does not appear to alter the electron density topological parameters of the hydrogen bond bond critical points (BCPs) by more than a few percent over and above the values for ve or six-membered rings, the effects on the environment of the oxygen atoms are profound as evidenced by the 17O chemical shielding tensors, and the 17O chemical shift, as described in the next section.
3.2 Chemical Shielding Tensors
Calculations in our laboratory of the absolute shielding tensor for 17O-water monomer in the gas-phase at the MPW1PW91/6-311+G(2d,p) level of theory have yielded a value of 327.3 ppm. This is excellent agreement with the rovibrationally corrected value of 327.7 ± 0.3 ppm arrived at by Vaara et al.
Traditionally, attempts at calculating the 17O-NMR chemical shift for liquid water modelled by water clusters at a quantum mechanical level have not achieved adequate accuracy compared to the experimental value for the ice Ih to gas-phase shift of 48.6 ppm14 . Indeed, use of self-consistent reaction eld (SCRF) methods such as the polarised continuum model (PCM) or COSMO not only fail to predict the correct magnitude for the 17O chemical shift but also give the wrong absolute sign, with up eld shifts for small clusters15–17 .
We have recently shown that ab initio quantum chemical methods using a combination of a hybrid density functional and a Pople triple split-valence basis set with diffuse and polarisation functions, is able to predict the full range of 17O chemical shift and, incidectally, also the 1H-proton chemical shift, on going from gas-phase water to ordered ice, so long as account is taken of water coordination geometry, lling all four hydrogen bonding donor-acceptor sites and ring cooperativity17.
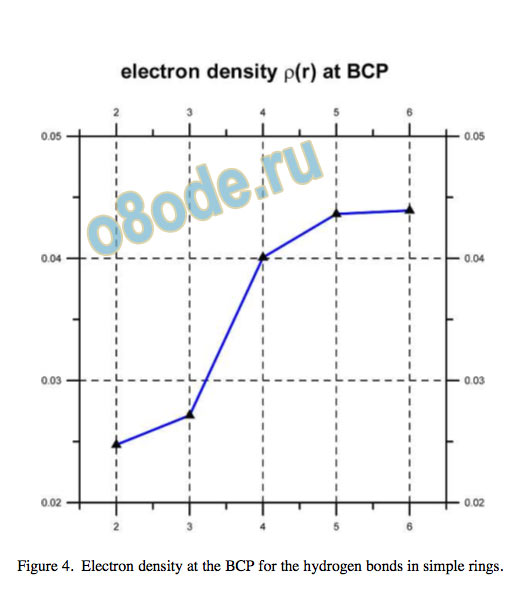
Figure 4. Electron density at the BCP for the hydrogen bonds in simple rings.
The 17O NMR chemical shielding tensors show a consistent decrease (chemical shift increases) as ring cooperativity and geometry improve and the water molecule is ultimately tetracoordinated with almost ideal tetrahedral sp3 symmetry. In this case, each water molecule has two O-H donors and two lone-pair acceptors occupied on the oxygen atom.
The asymptotic value for the 17O chemical shielding tensor approaches 272 ppm, giving a chemical shift compared to gas-phase water of 55 ppm. Our results are illustrated17 graphically in Fig. 5 and Fig. 6.
This calculated shift of 55 ppm is suf cient to account for the experimentally observed values. A deshielding (down eld shift) of 40 ppm is observed experimentally on going from vapour phase water at 100oC to liquid water at room temperature. Approximately a further 8 ppm deshielding takes place on going from liquid water to ice Ih, making in total some 48 ppm compared to the gas-phase value14 . At an electronic level, increasing cooperativity and enhanced tetrahedral coordination result in the oxygen atom becoming increasingly negatively charged, energetically stabilised, with an increased paramagnetic component to the shielding tensor and decreased shielding anisotropy, as the electric eld gradient (EFG) decreases.
Our explicit atomic level electronic model of ordered water molecules in liquid water and ice provides chemical shift values that are totally consistent with values obtained
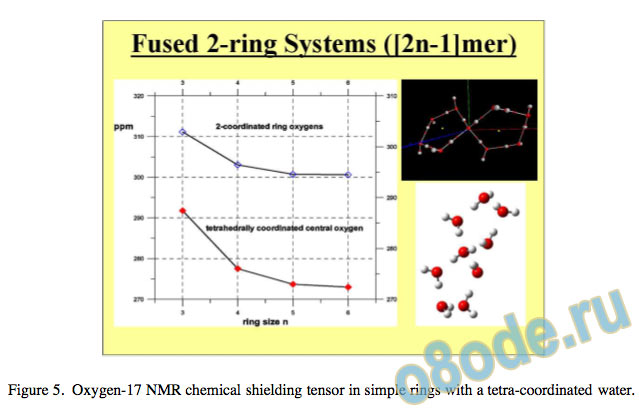
Figure 5. Oxygen-17 NMR chemical shielding tensor in simple rings with a tetra-coordinated water.
experimentally by NMR. In particular, since neither water vapour at 100oC is completely dissociated nor is ice completely ordered at 0oC, our results currently provide probably the most accurate model of the electronic environment of the oxygen atom in water permitting not only an explanation of the change in chemical shift on going from water vapour to liquid, and from liquid to ice, but also a quantitative explanation of the chemical shift temperature sensitivity in the range 0-100oC. The only other realistic chemical shift values for water have been provided by combined quantum mechanics and molecular dynamics, the CPMD approach of Car-Parrinello18 , as reported by Pfrommer et al.14 and Pennanen et al.19 . Whereas our ab initio cluster method provides an explicit snapshot of water order and its electronic environment, the CPMD approach provides a time average for a water molecule embedded in its solvation shell of neighbouring water molecules.
3.3 IR and Raman Spectroscopy
Cooperative effects in water clusters result in substantial red-shifts in both the IR and Raman spectra, often amounting to some hundreds of wave numbers. The example of the heptadecamer (n = 17) cluster is shown in Fig. 7. Increased red-shifting of the O–H stretching vibration is common to all systems in which extensive hydrogen bond cooperativity occurs20, 22, 21. In larger systems such as hydrated glucopyranose21 or water clusters the O–H vibrations are strongly synchronised or phase-locked. Scaled values of the IR and Raman frequencies for large water clusters are extremely good approximations to the experimental values and spectral shape for liquid water and ice, lying within a few percent of the spectroscopically determined value (unpublished data).
4 Conclusions
Tetrahedrally coordinated water clusters containing either the hexagonal or pentagonal ring motif, provide an explicit means of investigating theoretically the physics and physical chemistry of water at an atomic and electronic level, as found in nature as liquid water,
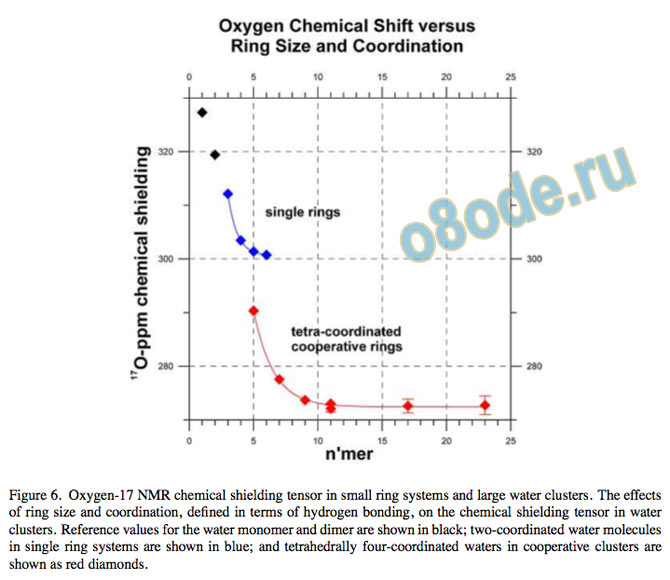
Figure 6. Oxygen-17 NMR chemical shielding tensor in small ring systems and large water clusters. The effects of ring size and coordination, de ned in terms of hydrogen bonding, on the chemical shielding tensor in water clusters. Reference values for the water monomer and dimer are shown in black; two-coordinated water molecules in single ring systems are shown in blue; and tetrahedrally four-coordinated waters in cooperative clusters are shown as red diamonds.
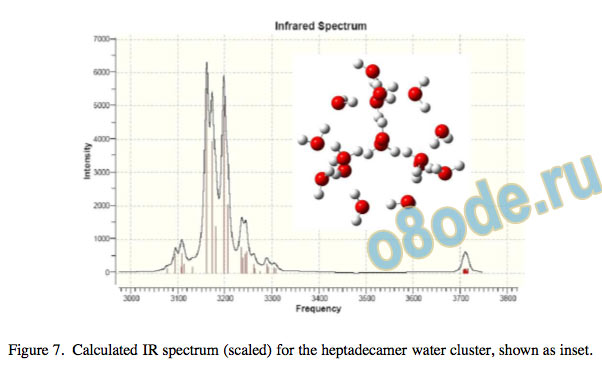
Figure 7. Calculated IR spectrum (scaled) for the heptadecamer water cluster, shown as inset. ice or in the form of gas hydrates. Water is an extremely polar liquid which shows extensive long-range order even in the uid phase, and is characterised by a network of highly cooperative hydrogen bonds giving rise to synchronisation of the O–H vibrational modes.
Clari cation of the detailed physical properties of water at atomic and sub-atomic level remains a pre-requisite to understanding its unique role as the solvent without which biological life as we know it would not exist.
Acknowledgments
I would like to thank the following colleagues with whom I have collaborated or held useful discussions during the course of the work reported here: Benedetta Mennucci (Pisa); Jacopo Tomasi (Pisa); Mark Zottola (Birmingham Alabama); Jose Sordo (Oviedo); Ernst Bause (Bonn). I should also like to acknowledge computer time on the IBMSC-JUMP machine made available in the form of of a project grant by the John Neumann Institute for Computing (NIC), Research Centre Julich.
References
1. Davidson,D. W.; Garg,S. K.; Gough,S. R.; Handa,Y. P.; Ratcliffe,C. I.; Ripmeester,J. A.; Tse,J. S.; Laboratory analysis of a naturally occurring gas hydrate from sediment of the Gulf of Mexico, Geochim. Cosmochim. Acta 50, 619–623 (1986).
2. Gas Hydrates on the Brink, Nature 420, 622–623 (2002).
3. Loveday, J. S.; Nelmes, R. J.; Guthrie, M.; Belmonte, S. A.; Allan, D. R.; Klug, D. D.; Tse, J. S.; Handa, Y. P.; Stable Methane Hydrate Above 2 GPa and the Source of Titan’s Atmospheric Methane, Nature 410, 661–663 (2001).
4. Stillinger, F. H.; Water revisited, Science 209, 451–457 (1980).
5. Soper, A. K.; Phillips, M. G.; A new determination of the structure of water at 25oC, Chem.Phys. 107, 47–60 (1980).
6. Soper, A. K.; Bruni, F.; Ricci, M. A.; Site-site Pair Correlation Functions of Water from 25oC to 400oC: Revised Analysis of New and Old Diffraction Data, J. Chem. Phys. 106, 247–254 (1997).
7. English, N. J.; Macelroy, J. M. D.; Structural and Dynamical Properties of Methane Clathrate Hydrates, J. Comp. Chem. 24, 1569–1581 (2003).
8. Kirchner, M. T.; Boese, R.; Billups, W. E.; Norman, L. R.; Gas Hydrate SingleCrystal Structure Analysis, J. Amer. Chem. Soc. 126, 9407–9412 (2004).
9. Nitzan, A.; Ulrafast relaxation in water, Nature 402, 472–475 (1999).
10. Woutersen, S.; Bakker, H. J.; Resonant intermolecular transfer of vibrational energy in liquid water, Nature 402, 507–509 (1999).
11. Bader, R. F.W.; Atoms in Molecules. A Quantum Theory (Oxford University Press, Oxford, UK, 1990).
12. Weinhold,F.; Landis,C. R.; Valency and Bonding. A Natural Bond Orbital DonorAcceptor Perspective (Cambridge University Press, Cambridge, UK, 2005).
13. Vaara, J.; Lounila, J.; Ruud, K.; Helgaker, T.; Rovibrational Effects, Temperature Dependence and Isotope Effects on the Nuclear Shielding Tensors of Water. A New Absolute Shielding Scale, J. Chem. Phys. 109, 8388–8397 (1998).
14. Pfrommer, B. G.; Mauri, F.; Louie, S. G.; NMR Chemical Shifts of Ice and Liquid Water. Effects of Condensation, J. Amer. Chem. Soc. 122, 123–129 (2000).
15. Chesnut, D B.; Structures, Energies and NMR Shieldings of Some Small Water Clusters on the Counterpoise Corrected Potential Energy Surface, J. Phys. Chem. A. 106, 6876–6879 (2002).
16. Tomasi, J.; Mennucci, B.; Cammi, R.; Quantum Mechanical Continuum Solvation Models, Chem. Rev. 105, 2999–3093 (2005).
17. Klein, R. A.; Mennucci, B.; Tomasi, J.; Ab Initio Calculations of 17O NMR-Chemical Shifts for Water. The Limits of PCM Theory and the Role of Hydrogen-Bond Geometry and Cooperativity, J. Phys. Chem. A 108, 5851–5863 (2004).
18. Car, R.; Parrinello, M.; Uni ed Approach to Molecular Dynamics and Density Functional Theory, Phys. Rev. Lett. 55, 2471–2474 (1985).
19. Pennanen, T. S.; Vaara, J.; Lantto, P.; Sillanpaa, A. J.; Lassonen, K.; Jokisaari, J.; Nuclear Magnetic Shielding and Quadrupole Coupling Tensors in Liquid Water. A Combined Molecular Dynamics Simulation and Quantum Chemical Study, J. Amer. Chem. Soc. 126, 11093–11102 (2004).
20. Klein, R. A.; Ab Initio Conformational Studies on Diols and Binary Diol-Water Systems Using DFT Methods. Intramolecular Hydrogen Bonding and 1:1 Complex Formation with Water, J. Comp. Chem. 23, 585–599 (2002).
21. Klein, R. A.; Electron Density Topological Analysis of Hydrogen Bonding in Glucopyranose and Hydrated Glucopyranose, J. Amer. Chem. Soc. 124, 13931–13937 (2002).
22. Klein, R. A.; Hydrogen Bonding in Diols and Binary Diol-Water Systems Investigated Using DFT Methods. II. Calculated Infrared OH-Stretch Frequencies, Force Constants, and NMR Chemical Shifts Correlate with Hydrogen Bond Geometry and Electron Density Topology. A Reevaluation of Geometrical Criteria for Hydrogen Bonding, J. Comp. Chem. 24, 1120–1131 (2003).