Surface States of Excess Electrons on Water Clusters

Поверхностное состояние электронов в водяных кластерах

R. N. Barnett, Uzi Landman, and C. L. Cleveland

School of Physics, Georgia Institute of Technology, Atlanta, Georgia 30332

and Joshua Jortner

School of Chemistry, Tel Aviv University, 69978 Tel Aviv, Israel (Received 29 April 1987)

Electron attachment of water clusters was explored by the quantum path-integral molecular-dynamics method, demonstrating that the energetically favored localization mode involves a surface state of the excess electron. The cluster size dependence, the energetics, and the charge distribution of these novel electron-cluster surface states are explored.

PACS numbers: 73.20.At, 36.40.+d, 61.20.Ja, 71.55.Jv

Most studies1 of small clusters focus on the dependence of the geometry, level structure, and other properties upon size (number of particles) and the "transition" from molecular to condensed-matter behavior. Characteristic to these systems is a large surface-to-volume ratio which could lead to unique, qualitatively different from bulk, chemical and physical behavior.2'3 In this Letter we shall demonstrate, using quantum path-integral molecular-dynamics simulations3'4 (QPIMD), that the energetically stable excess-electron states in small water clusters5"7 involve surface states rather than internally localized states which may be regarded as precursors of the celebrated hydrated electron.8

The existence of the solvated electron was experimentally demonstrated in 1863 for liquid ammonia,9 and in 1962 for water.8 The localization of an excess electron in the bulk of a polar fluid originates from the combination of longand short-range attractive interactions,10 and is accompanied by a large local molecular reorganization. Nonreactive electron localization in water clusters was experimentally documented to originate either from electron binding during the cluster nucleation process,5,6 or by electron attachment to preexisting clusters.7 The occurrence of a weakly bound state in (H20)2~ (vertical electron binding energy —3 meV for the equilibrium state,11,12 and —13 to —27 meV for a persistent metastable state),11 characterized by a diffuse excess electron charge distribution (radius of gyration of — 36tfo), can be understood, on the basis of QPIMD calculations, to originate from weak electron-dipole interactions. On the other hand, the existence of stable (H20)„(n > 11) clusters,5"7 which are characterized6 by a large vertical electron affinity, i.e., 0.75 eV (for n = \l) to 1.12 eV (for n = \9), poses a challenging theoretical problem. Quantum-mechanical calculations13,14 for (H20)6~ and (H20)8" reveal that the adia-batic electron affinity of these, and presumably also larger, water clusters will be negative, precluding the existence of such stable excess-electron clusters, in contrast with experiment.5"7 These theoretical studies followed faithfully the conventional wisdom in the field of solvated-electron theory,10 invoking the implicit assumption that the excess-electron state in (H20)n_ constitutes an interior localization mode. QPIMD calculations are ideally suited to explore alternative localization modes of the excess electron in water clusters.

The QPIMD method rests on an isomorphism between the quantum problem and a classical one, wherein the quantum particle is represented by a necklace of P pseu-doparticles ("beads") with nearest-neighbor harmonic interactions.3,4 If we invoke previous formalism and notation3 the average total energy of the system is

with K =3/2/3 + Kmi, where Vc is the interaction potential between the classical particles (whose number is TV), is the cluster-electron interaction for the z'th pseu-doparticle,

P = \/kT, and angular brackets indicate statistical averaging. The water molecules in this study were treated classically. The choice of the number, P, of beads representing the excess electron is temperature dependent. As a rule of thumb, adequate discretization is achieved for PkT> e2/ao.

A key issue in modeling the system is the choice of interaction potentials. Fortunately, for neutral small water clusters, interaction-potential functions which provide a satisfactory description for a range of properties are available. We have used the RWK2-M model15 for the intramolecular and intermolecular interactions. For the electron-water interaction we have constructed a pseudo-potential (Fig. 1) in the spirit of the density-functional theory, which consists of Coulomb, polarization, exclusion, and exchange contributions:

K(r„R0,Ri,R2) = KCoui+ Vp + Ve + Vx. (1)

FIG. 1. Contours of electron-water interaction, left, and the electron density [logiop(r)], right, [see Eq. (4)1 in the plane containing the nuclei. The oxygen is located at the origin.

The positions of the oxygen and hydrogen nuclei of the water molecule are given by (Ro,Ri,R2) and Te is the position of the electron. The Coulomb interaction is

where R3 =Ro + (Ri +R2 ~~2R0)<S is the position of the negative point charge of the RWK2-M model and Rcc =0.5tfo. The values q \ =qi =0.6e, q3= — \.2e, 5=0.221 837 56a0 were chosen15 to give a good representation of the dipole and quadrupole moments of H2O. The polarization interaction is given by

where a =9.7446 a.u. is the spherical polarizability of the water molecule. The form of Vp and the value of Rp^ 1.6#o were chosen to fit the adiabatic polarization potential as calculated by Douglass et alX6 The exclusion, Ve, and exchange, Vx, contributions both require the electron density, p(r,Ro,Ri,R2), of the water molecule17 which, in the regions of importance, is adequately approximated by the simple expression (see Fig. 1)

The repulsion, due to the exclusion principle, is modeled as a "local kinetic-energy" term,18

The exchange interaction is modeled via the local exchange approximation,

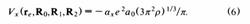
The parameter ax was taken to be ax=0.3 in order to obtain good agreement between our simulation results and the self-consistent field results of Rao and Kestner13 for (H20)8~ at a fixed configuration of the water molecules.

Equipped with these potentials, we have embarked upon an investigation of the energetics and geometry of (H20)„~ (/7=8-18) clusters. In correspondence with the alternative experimental preparation methods5"7 we invoked two initial conditions: (i) first condensing the water molecules around a classical negatively charged particle with a radius of 5ao, and subsequently replacing the classical particle with the electron necklace; (ii) placing a compact distribution of beads next to an equilibrated neutral cluster. For the smaller clusters n < 12 a surface state develops rapidly, regardless of the initial setup of the calculation, while for « = 18, (i) and (ii) yield an "internal" and "surface" state, respectively.

In Table I we summarize the energetic data for the vertical electron affinity, — Aey =U(e-(H20)n) +Kmi, where U is the averaged interaction-potential energy between the electron and the water molecules, the cluster reorganization energy, Ec, and the electron adiabatic electron affinity, Ae,A =Ae^v — Ec. The neutral-cluster reference states were obtained by simulated annealing. The lowest-energy configuration for each cluster size was then used to calculate Ec (the difference between the in-termolecular and intramolecular potential energies in the negatively charged and neutral-cluster configurations). The energetic stability of the negatively charged cluster with respect to the equilibrium neutral cluster plus free

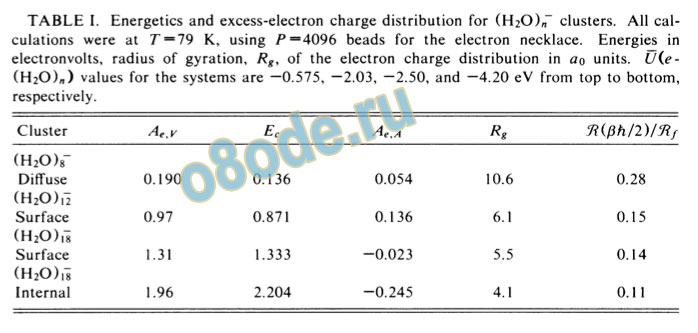
TABLE I. Energetics and excess-electron charge distribution for (H20),T clusters. All calculations were at T~19 K, using />=4096 beads for the electron necklace. Energies in electronvolts, radius of gyration, Rgy of the electron charge distribution in ao units. U(e-(H20)„) values for the systems are —0.575, —2.03, —2.50, and —4.20 eV from top to bottom,
respectively.

electron is inferred from the magnitude and sign of Ae,A (positive values corresponding to a stable bound state). The bead distributions for the excess electron (Fig. 2) are characterized by the radius of gyration, Rg = y P ~2(£/j; (r,■— Tj)2), and the degree of localization by the complex time-correlation function19 3Kt — t') -<|r(*)-r(f')|2>1/2 for * -1' e (0,0ft), yielding the correlation length Ji(fih/2) (Table I), which for a free particle is denoted by 3if — -J3XT/2, where XT is the thermal wavelength of the particle. All calculations were at constant temperature with the velocity form of the Verlet integration algorithm.20,21
From these results we assert that there is a remarkable quantitative difference between internal and surface

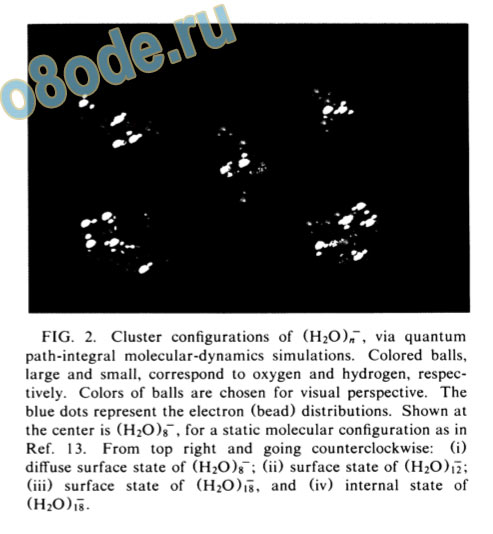
FIG. 2. Cluster configurations of (H20),T, via quantum path-integral molecular-dynamics simulations. Colored balls, large and small, correspond to oxygen and hydrogen, respectively. Colors of balls are chosen for visual perspective. The blue dots represent the electron (bead) distributions. Shown at the center is (H20)g~, for a static molecular configuration as in Ref. 13. From top right and going counterclockwise: (i) diffuse surface state of (H20)8~; (ii) surface state of (H20)i^; (iii) surface state of (H20)ii, and (iv) internal state of (h20)i8.

states of the excess electron in water clusters. The value of Ec is considerably lower for a surface state than for an internal state insuring relative energetic stability of the former (Table I). As is apparent for (H20)i8, Aeyy is considerably higher (and outside the range of the experimental values) for the interior state; however, the high value of Ec results in Ae A = —0.245 eV, precluding a stable internally localized state. On the other hand, for the electron surface state of (H20)f8 the value of Ae,A is closer to zero (and the value of AP y is in the range of measured values), favoring this mode of localization. For (H20)i~2 (Table I and Fig. 2), only a surface state is found. Finally, for (H20)8~, a very small electron binding energy is found and the state is characterized by a diffuse charge distribution (Fig. 2 and Table I).

From these results we conclude as follows: (1) The electron-localization mode in (H20)„clusters involves the formation of a surface state. (2) The onset of electron localization in a tightly bound state in (H20)w~ clusters is exhibited for n > 8, in accord with experiment5"7 (n > 11). (3) The vertical electron binding energies for the cluster-electron surface state in (H20)il> and (H20)i"g (Table I) are in adequate agreement with the experimental photoelectron spectroscopic data.6 Additionally, Aey rises sharply in the range «=8-12. For the (H20)8~ cluster the diffuse nature of the excess-electron distribution could lead to a large collision-induced electron-detachment cross section, which may account for the absence of n < 11 clusters from the experimental spectra.5"7 Considering the complexity of the system, statistical uncertainties, and those implicit in the model interaction potentials, we are encouraged by our results which provide a consistent energetic and structural picture of electron localization in small water clusters.

We have demonstrated the prevalence of the surface localization mode in (H20)„~ clusters, which is qualitatively different from the localization mode of the hydrat-ed electron in the bulk. Consequently, we infer that long-range attractive interactions play an important role
in electron localization in the bulk. In this context we conjecture that the striking difference between the lowest coordination number for electron localization in water (n > 11) and that in ammonia (az > 35) clusters may originate from a weaker electron-molecule interaction in ammonia, which renders the surface state unstable in (NH3),,for small n. Consequently, localization may require in this case the buildup of long-range attractive interactions thus resulting in large coordination numbers.

Useful conversations with Neil Kestner and remarks on the manuscript by Andy Zangwill are gratefully acknowledged. This research was supported by U.S. Department of Energy Grant No. FG05-86ER45234 (U.L.) and by the U.S.-Israel Binational Science Foundation (U.L. and J.J.).

^er. Bunsenges. Phys. Chem. 88 (1984); Surf. Sci. 156 (1985).
2R. L. Whetten, D. M. Cox, D. J. Trevor, and A. Kaldor, Phys. Rev. Lett. 54, 1494 (1985); M. E. Geusic, M. D. Morse, and R. D. Smalley, J. Chem. Phys. 82, 590 (1985).
3U. Landman, D. Scharf, and J. Jortner, Phys. Rev. Lett. 54, 1860 (1985).
4D. Chandler and P. G. Wolynes, J. Chem. Phys. 74, 4078 (1981); M. Parrinello and A. Rahman, J. Chem. Phys. 80, 860 (1984).
5H. Haberland, H. G. Schindler, and D. R. Worsnop, Ber. Bunsenges. Phys. Chem. 88, 3903 (1984), and J. Chem. Phys. 81, 3742 (1984).
6J. V. Coe, D. R. Worsnop, and K. H. Bowen, to be published.
7M. Knapp, O. Echt, D. Kreisle, and E. Recknagel, J. Chem. Phys. 85, 636 (1986), and J. Phys. Chem. 91, 2601 (1987). 8E. J. Hart and J. W. Boag, J. Am. Chem. Soc. 84, 4090
(1962).
9W. Weyl, Ann. Phys. (Leipzig) 197, 601 (1863).
10J. Jortner, J. Chem. Phys. 30, 839 (1959); D. A. Copeland, N. R. Kestner, and J. Jortner, J. Chem. Phys. 53, 1 189 (1970).
11U. Landman, R. N. Barnett, C. L. Cleveland, D. Scharf, and J. Jortner, J. Phys. Chem. (to be published).
12A. Wallquist, D. Thirumalai, and B. J. Berne, J. Chem. Phys. 85, 1583 (1986).
13B. K. Rao and N. R. Kestner, J. Chem. Phys. 80, 1587 (1984), and references therein.
14N. R. Kestner and J. Jortner, J. Phys. Chem. 88, 3818 (1984); M. D. Newton, J. Chem. Phys. 58, 5833 (1973).
,5J. R. Reimers, R. O. Watts, and M. L. Klein, Chem. Phys. 64, 95 (1982); J. R. Reimers and R. D. Watts, Chem. Phys. 85, 83 (1984). This paper, as well as the description of the potential in the first one [Eq. (13) and Table l], contains several ambiguities and typographical errors. When these are corrected we reproduce their results.
16C. H. Douglass, Jr., D. A. Weil, P. A. Charlier, R. A. Eades, D. G. Truhlar, and D. A. Dixon, in Chemical Applications of Atomic and Molecular Electrostatic Potentials, edited by P. Politzer and D. G. Truhlar (Plenum, New York, 1981), p. 173.
17C. W. Kerr and M. Karplus, in Water, edited by F. Franks (Plenum, New York, 1972), p. 21; M. W. Ribarsky, W. D. Luedtke, and U. Landman, Phys. Rev. B 32, 1430 (1985).
18J. N. Bardsley, Case Stud. At. Phys. 4, 299 (1974); G. G. Kleiman and U. Landman, Phys. Rev. B 8, 5484 (1973).
19A. L. Nichols, D. Chandler, V. Singh, and D. M. Richardson, J. Chem. Phys. 81, 5109 (1984).
20J. R. Fox and H. C. Anderson, J. Phys. Chem. 88, 4019 (1984).
21 In the QPIMD method the averaged results do not depend on the dynamic masses used to generate the classical trajectories. We used a mass of 1 amu for the classical particles, and 0.025 amu for the beads. The integration time step was 2.625 x 10 ~16 sec. Prior to averaging, the systems evolved until no discernible trend was observed. Averaging was then performed typically over 2x 104 time steps.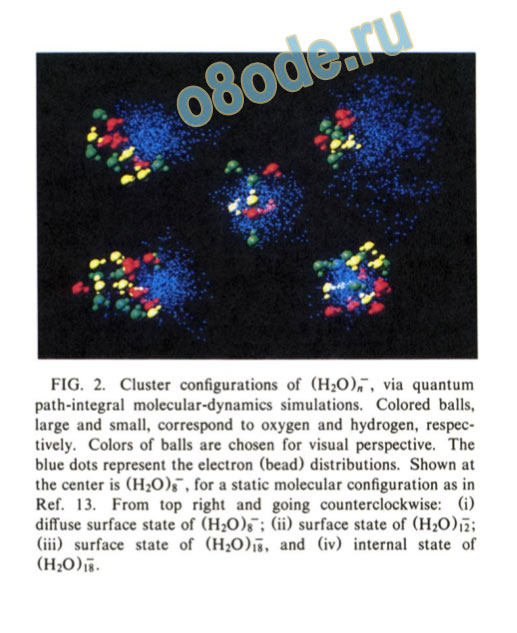

FIG. 2. Cluster configurations of (H20)„~, via quantum path-integral molecular-dynamics simulations. Colored balls, large and small, correspond to oxygen and hydrogen, respectively. Colors of balls are chosen for visual perspective. The blue dots represent the electron (bead) distributions. Shown at the center is (H^COg-, for a static molecular configuration as in Ref. 13. From top right and going counterclockwise: (i) diffuse surface state of (HjO)*-; (ii) surface state of (H2CO12; (iii) surface state of (H2CO18, and (iv) internal state of (H20),i.