Научные доказательства кластерной структуры воды
Раздел подготовлен Мосиным О.В.
В этом разделе собраны иинтересные научные статьи по структуре воды, написанные зарубежными учёными (на русском языке таких материалов или очень мало, или нет вообще). Все эти статьи я с большим трудом отыскал в интернете и скачал с сайтов зарубежных научных журналов. Эти материалы действительно уникальны по своей научной значимости, поскольку их результаты доказывают кластерную структуру воды. Материалы уникальные тем, что это полные статьи. Обычно научные журналы не публикуют полнотекстные статьи, а дают лишь короткую аннотацию. Поэтому найти полноценные научные статьи в интернете довольно сложно. Нужно либо идти в научную библиотеку или платить деньги интернет-редакциям. Поэтому это будет очень полезно нашим читателям и особенно людям, работающей в научной сфере, так как таких статей на русском языке практически нет. Меня очень часто читатели спрашивают тот или иной физико-химический показатель, а здесь все они собраны воедино.
Мосин Олег
Water clusters:
Untangling the mysteries of the liquid, one molecule at a time
Frank N. Keutsch and Richard J. Saykally Department of Chemistry, University of California, Berkeley, CA 94720-1460
This contribution is part of the special series of Inaugural Articles by members of the National Academy of Sciences elected on April 27, 1999.
Contributed by Richard J. Saykally, May 29, 2001
Extensive terahertz laser vibration-rotation-tunneling spectra and mid-IR laser spectra have been compiled for several isotopomers of small (dimer through hexamer) water clusters. These data, in conjunction with new theoretical advances, quantify the structures, force elds, dipole moments, and hydrogen bond rearrangement dynamics in these clusters. This new information permits us to systematically untangle the intricacies associated with cooperative hydrogen bonding and promises to lead to a more complete molecular description of the liquid and solid phases of water, including an accurate universal force eld.
The quest to achieve an accurate description of liquid water has produced major advances in the last t wo decades (1), yet despite the constr uction of hundreds of model force fields for use in simulations, the great advances in comput ational technolog y, and the development of power ful ab initio molecular dynamics methods, we remain unable to accurately calculate the properties of liquid water (e.g., heat capacit y, densit y, dielectric const ant, compressibilit y) over significant ranges in conditions (2). We do not yet have a satisfactor y molecular description of how a proton moves in the liquid, we do not fully underst and the molecular nature of the sur faces of either ice or liquid water (3), nor do we underst and the origin of the intriguing anomalies and singularities found in the deeply supercooled region (4). Although it is clear that the hydrogen bond net work and its f luctuations and rearrangement dynamics deter mine the properties of the liquid, no experiment al studies ex ist that reveal det ailed infor mation on a molecular level without considerable interpret ation (5). Moreover, the reliabilit y of water models for simulating solvation phenomena and biological processes remains relatively untested. A principal obst acle to resolv ing these issues is that of correctly describing the many-body, or cooperative nature of the hydrogen bonding interactions among a collection of water molecules. Theoretical work has shown that the H-bond is dominated by electrost atic interactions, balanced by the repulsive electron exchange, but that dispersion makes an appreciable contribution, whereas induction (polarization) is the dominant many-body ef fect (6, 7). It has proven notoriously dif ficult to accurately parameterize these interactions f rom ab initio calculations. Moreover, the ab initio molecular dynamics methods are based on densit y functional methods that explicitly omit the dispersion, and its expense mandates rather small sample sizes (e.g., 64 molecules) in simulations (8). But perhaps the central obst acle to developing quantit atively accurate and general methods has simply been the lack of a suit ably precise dat a set with which to test and calibrate theoretical approaches.
The central goal of the research rev iewed below is to advance the cause for accurately describing water in all its phases over arbitrarily large ranges of conditions, and the central contribution of our group has been to develop and apply novel methods of laser spectroscopy for the highly det ailed study of water clusters to prov ide such a dat a set. Recently, we also have initiated studies of the hydrogen bond breaking dynamics in water clusters and comparison of them with mechanisms proposed to prevail in liquid water.
Terahertz Laser Vibration-Rotation-Tunneling (VRT) Spectroscopy of Clusters
The first far-IR (FIR) spectra of gaseous water clusters were measured near 22 cm1 (455 m) by Busarow et al . in 1989 (9). The spectra consisted of 56 Ka 2 4 1 rot ation-tunneling transitions of (H2O)2, which complemented the microwave dat a (10, 11) obt ained by the pioneering work of Dyke et al . (10), in obt aining an accurate description of the dimer ground st ate. Zwart et al . (12) subsequently extended these dat a to other quantum st ates. Af ter some import ant technical developments that extended the operating range of the spectrometer to higher f requencies, Pugliano and Saykally (13) first measured an intermolecular VRT spectr um of a water cluster in 1992, with the detection of a torsional v ibration of the D2O trimer near 89.5 cm1 (112 m) (Fig. 1) (14 –16). This striking spectr um exhibited an exact symmetric rotor pattern, and ever y rot ational line was split into a distinctive quartet pattern that we now know results f rom quantum tunneling v ia t wo dif ferent hydrogen bond pathways connecting 48 degenerate minima on the 12-dimensional inter molecular potential sur face. Pugliano et al . (17) quickly followed with the first obser vation of a dimer inter molecular v ibration (acceptor t wist), near 83 cm1 (120 m).
Subsequent work at Berkeley by Liu et al . (18) produced much more extensive trimer spectra and the first det ailed assignment of the transitions. Cr uzan et al . (19) discovered VRT spectra of the tetramer shortly af ter ward, and Liu et al . followed with the detection of the pent amer (20) and hexamer (21). Recent ef forts have produced highly det ailed characterizations of both the dimer and trimer, as well as greatly expanded dat a for the other clusters (22–27). We describe the current underst anding of the dimer through hexamer clusters that has been achieved f rom these dat a, and through the ef forts of many concurrent theoretical studies, in a later section.
IR Cavity Ringdown Spectroscopy
While mid-IR spectra of water clusters had been obser ved by the Pimentel group in matrix studies in 1957 (28), the OH stretching v ibrations of gaseous water clusters were first studied indirectly in 1982 by Vernon et al . (29) in IR predissociation experiments in supersonic beams, and shortly af ter that by Page et al . (30). Vernon et al . assigned the spectra to (H2O)n, n 1–5, and recorded a narrow transitions (15 cm1) at 3,715 cm1, which they attributed to the f ree OH stretch in cyclic water clusters, and a much broader feature (200 cm1) at lower f requency that they attributed to the bound OH stretch. Page et al . concentrated on the water dimer, finding four peaks, including the bound OH stretch, a broad transition at 3,545 cm1, red-shif ted f rom the f ree monomer OH stretches. Coker et al . (31) found four dimer OH stretch f requencies identical to those deter mined by Page Abbreviations: VRT, vibration-rotation-tunneling; FIR, far-IR; ASP, anisotropic site potential; IPS, intermolecular potential surface.
Present address: Department of Chemistry and Chemical Biology, Harvard University, Cambridge, MA 02138.
To whom reprint requests should be addressed. E-mail: saykally@uclink4.berkeley.edu. www.pnas.orgcgidoi10.1073pnas.191266498 PNAS September 11, 2001 vol. 98 no. 19 10533–10540
et al . and also identified larger clusters in supersonic expansions carr ying increasing concentrations of water. Huang and Miller (32, 33) reported the first rot ationally resolved spectr um of (H2O)2 and obser ved the four OH stretch v ibrations, and recently Frochtenicht et al . (34) used a size selection technique in which a He beam is used to eject clusters f rom a molecular beam as a function of their size. They were able to measure the f ree and bound OH stretching f requencies for clusters up to the pent amer.

The wide tuning range of our IR cav it y ringdown laser absorption spectrometer recently per mitted the first det ailed studies of both the covalent bending v ibrations of H2O clusters (35), which occur near 1,600 cm1, and the stretching v ibrations of D2O clusters (36, 37), which fall near 2,700 cm1 (Fig. 2). All of the obser ved clusters except the dimer exhibit strong v ibrational predissociation broadening of their OD stretch spectra that obscures rot ation-tunneling features. For the D2O dimer, however, the ac ceptor antisy mmetric stretch exhibits wellresolved acceptor switching doublets for each rot ational line, whereas the donor stretch exhibits rot ational lines that are broadened, but by about 30 times less than found for the H2O isotopomer (36, 37). All bands obser ved for the cluster HOH bending v ibrations are severely broadened, implying a stronger coupling with the dissociation coordinate (35). The sharp rot ation-tunneling str ucture measured for (D2O)2 (Fig. 2b) was import ant for the deter mination of the dimer potential sur face (38, 39), because the acceptor switching splittings cannot be deter mined directly in the FIR experiments because of prohibitive selection r ules. With the use of theoretical integrated band intensities, these cav it y ringdown measurements per mitted the first deter mination of the absolute water cluster concentrations in a supersonic beam (40). Interestingly, the trimer dominates the cluster distribution for both H2O and D2O. This domination is probably caused by the discontinuous increase in the permonomer binding energ y (D0), which jumps f rom 12 D0 to D0 f rom dimer to trimer, while increasing much more slowly for larger clusters.
The Evolution of Hydrogen Bonding in Small Water Clusters The archet ype of the H-bond in water is the water dimer (Fig. 3). The OOO dist ance, ref lecting the length of the H-bond is Fig. 1. The 89.5 cm1 torsional hot band of (D2O)3 (Left) was the rst intermolecular vibrational band observed for a water cluster in the gas phase (13). The spectrum shows splitting of each vibration-rotation transition into a characteristic quartet by the bifurcation tunneling motion (see Fig. 6b). (Right) Shown is this quartet for the 41.1 cm1 torsional band (103), the most intense water trimer band observed to date. The intensities of the quartet components are determined by nuclear spin weights. SN, Signal to noise. Fig. 2. The IR-cavity ringdown laser absorption spectrometer spectrum of the OD stretch region of D2O is shown (a). The spectrum shows vibrational bands due to the stretch of the free OD at the highest frequencies. Below 2,700 cm1 the OD stretch frequencies of the bound OD groups are observed on top of a weak broad absorption from an amorphous ice-like phase. The bound OD stretch frequencies decrease with increasing cluster size (40). The IR-cavity ringdown laser absorption spectrometer spectrum of the (D2O)2 acceptor antisymmetric OD stretch (b) shows the clearly resolved acceptor switching splitting. This splitting is most readily observable in the intense Q-branch transitions (36). This observation has allowed the determination of the acceptor switching splitting in the vibrational ground state, which was not possible with the previously existing data.

Fig. 3. The equilibrium structure of the water dimer as determined by calculations on the VRT(ASP-W)-II potential surface (R. S. Fellers, M. G. Brown, L. B. Braly, M. Colvin, C. Leforestier, and R.J.S., unpublished work). The hydrogen bond deviates 2.3° from linearity, the OOO distance is 2.952 Å, and the bond strength, D0, is 3.40 kcalmol. The highly nonrigid dimer has six oppy intermolecular vibrations.
Fig. 4. The water dimer exhibits three distinct low barrier tunneling pathways that rearrange the hydrogen bonding pattern. Acceptor switching (AS), having the lowest barrier of all tunneling motions estimated at 157 cm1 by VRT(ASP-W), is the most facile tunneling motion. This tunneling pathway exchanges the two protons in the hydrogen bond acceptor monomer and has been determined to begin with a ip of the acceptor monomer followed by a rotation of the donor monomer around its donating OOH bond, and completed by a 180° rotation of the complex about the OOO bond. The tunneling motion splits each rovibrational energy level into two. Interchange tunneling (I) exchanges the roles of the hydrogen bond donating and accepting water monomers. Several possible pathways exist for this exchange, the lowest barrier path being the geared interchange motion. This pathway begins with a rotation of the donor in the D angle and rotation of the acceptor about its C2 axis to form a trans transition state structure. This is followed by a rotation of the initial donor about its C2 axis and a rotation of the initial acceptor in the A angle such that it becomes the donor. The pathway is completed by a 180° end-over-end rotation of the complex.
Calculations with the VRT(ASP-W) potential determine the barrier to be 207 cm1. The anti-geared interchange pathway also has been determined to be important and is similar to the geared pathway except that it has a cis transition state. The tunneling motion splits each energy level by a much smaller amount than the acceptor switching resulting into two sets of three energy levels. The bifurcation tunneling motion B, wherein the hydrogen bond donor exchanges its protons, consists of the simultaneous in plane librational motion of the donor with the ip of the acceptor monomer. This is the highest barrier tunneling pathway [394 cm1 with VRT(ASP-W)] resulting in a small shift of the energy levels.
10534 www.pnas.orgcgidoi10.1073pnas.191266498 Keutsch and Saykally 2.952 Å, and the hydrogen bond strength (dissociation energ y) of (H2O)2 is 3.09 kcalmol, corresponding to the zero-pointcorrected binding energ y (De) of 4.85 kcalmol. The dimer equilibrium str ucture was deter mined in the potential sur face fit described below, wherein a ver y extensive dat a set encompassing five of the six fundament al inter molecular v ibrations with complete resolution of rot ation and hydrogen bond tunneling ef fects, have been fit to Stone’s highly det ailed anisotropic site potential (ASP) potential for m (38). Three distinct quantum tunneling processes (Fig. 4), for which the potential barriers all have been deter mined, rearrange the H-bond on time scales ranging f rom about 1 s to 1 ps (38). The tunneling motions connect eight degenerate minima on the inter molecular potential sur face (IPS), splitting each rov ibrational transition into six subbands.
The highest barrier (1.13 kcalmol, zero point corrected) process corresponds to the exchange of the bound and f ree hydrogen atoms on the donor molecule (bifurcation) and turns out to be the most facile means of breaking the H-bond, which has interesting implications with respect to bond-breaking dynamics in bulk water (5, 41). All six fundament al inter molecular v ibrations except for the out-of-plane libration have now been measured for both (H2O)2 and (D2O)2.
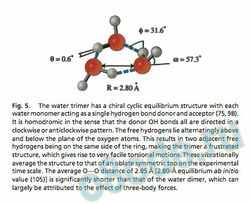
Each monomer in the water trimer acts both as a single donor and single acceptor of an H-bond, and each has one bound and one f ree hydrogen. Because of the alternation of the f ree hydrogen atoms above and below the plane of the ox ygens, this str ucture is chiral, as are those of all the odd-membered rings. Two distinct tunneling processes operate to rearrange the Hbond net work, here connecting 48 degenerate minima on the IPS (43, 44). The first is f lipping, which is essentially barrierless (Fig. 6a) (45), and the same bifurcation process described above for the dimer (Fig. 6b). This latter motion turns out to be a highly local one, with an uncorrected barrier near 2 kcalmol(43, 44).
These rearrangement pathways were systematically described in Fig. 5. The water trimer has a chiral cyclic equilibrium structure with each water monomer acting as a single hydrogen bond donor and acceptor (75, 98). It is homodromic in the sense that the donor OH bonds all are directed in a clockwise or anticlockwise pattern. The free hydrogens lie alternatingly above and below the plane of the oxygen atoms. This results in two adjacent free hydrogens being on the same side of the ring, making the trimer a frustrated structure, which gives rise to very facile torsional motions. These vibrationally average the structure to that of an oblate symmetric top on the experimental time scale. The average OOO distance of 2.85 Å [2.80-Å equilibrium ab initio value (105)] is signicantly shorter than that of the water dimer, which can largely be attributed to the effect of three-body forces.

Fig. 6. Two distinct tunneling pathways rearrange the hydrogen bond pattern in the cyclic water trimer. The torsional (ipping) motion (a) of the free hydrogens atoms from one side of the plane determined by the oxygen atoms to the opposing side connects two degenerate minima on the IPS. The barrier for this tunneling motion is lower than the vibrational zero-point energy for (H2O)3 and close to the vibrational zero-point energy for (D2O)3 (43, 44, 104). Inclusion of ipping of all free hydrogens splits each torsional energy level into a manifold of six states. This ipping motion is symmetrically equivalent to rotation around the axis and hence is a pseudorotational motion coupling strongly to the overall rotation of the cluster, which results in severe Coriolis perturbations that can be readily observed in all torsional bands.
Development of a detailed Hamiltonian accounting for this coupling was necessary for a complete understanding of the torsional states and analysis of the torsional bands (42). The bifurcation tunneling motion (b) in the water trimer consists of the exchange of a free and a bound hydrogen together with the ipping motion of the free hydrogens on the two neighboring water monomers. The bifurcation tunneling pathway is the lowest energy hydrogen bond breaking motion observed in water clusters, and, in the trimer, connects eight degenerate minima on the IPS, splitting each rovibrational transition into a quartet with relative intensities determined by the nuclear spin statistics. The barrier for this tunneling motion is about 2 kcalmol and thus results in much smaller splittings than does the torsional tunneling motion (43, 45).
Fig. 7. The FIR spectrum of liquid D2O and H2O are shown together with the D2O and H2O cluster data in the translational (100 –200 cm1) and librational (300 –1,000 cm1) band region. (Center Left) A stick spectrum of the 142.8 cm1 degenerate antisymmetric stretch band of (D2O)3. (Top Left) A scan of the RR2(2) transition, representative of the strongest observed rovibrational transitions. The 142.8 cm1 band lies well within the translational band of the liquid. No bifurcation tunneling splittings are observed, indicating that they are unchanged with respect to the ground state. (Center Right) The out-ofplane librational band of (H2O)3. Three parallel bands of (H2O)3 centered at 517.2, 523.9, and 525.3 cm1 were assigned. Theory predicts only one parallel trimer band for the whole librational band region. The subbands were explained by a dramatic (1,000) increase of tunneling splitting through the bifurcation pathway. (Top Right) A scan of the Q-branch of the 523.9 cm1 subband is shown and from the observed relative intensities the rotational temperature can be estimated at 5 K.
Keutsch and Saykally PNAS September 11, 2001 vol. 98 no. 19 10535
elegant work by Walsh and Wales (44). The water trimer VRT dat a set is the most extensive ex isting for any water cluster, with seven, four, and six complete inter molecular v ibrational bands obser ved for (D2O)3, (H2O)3, and mixed isotopomers, respectively. We have now achieved a ver y complete description of the low-f requency (100 cm1) torsional modes in the trimer (42, 46, 47), and have measured extensive VRT spectra in the translational (26) (about 150 cm1, Fig. 7) and librational (27) (about 520 cm1, Fig. 7) band regions as well. Thus, all of the features of liquid water that appear in the inter molecular v ibrational region ( 10 m) also ex ist for the trimer and have been quite well characterized.
The H-bonding motif of the water tetramer is similar to that of the trimer, with each monomer acting as a single donor and acceptor, and hav ing one f ree and one bound H (Fig. 8). The average OOO dist ance is further shortened to 2.79 Å. Interestingly, the water tetramer turns out to be more dif ficult to characterize than the trimer, as a result of its higher (S4) symmetr y (19, 24, 48, 49). Whereas the torsional motion of the f ree hydrogens in the trimer is ver y facile and results in a large number of low-f requency v ibrational bands (100 cm1), the only inter molecular v ibration of the tetramer obser ved below 100 cm1 both in (D2O)4 and (H2O)4 corresponds to the in-plane ring defor mation. The lowest f requency v ibrational band involving torsional st ates was obser ved at 137.8 cm1 in (D2O)4 compared with the lowest torsional st ate of (D2O)3 at 8.5 cm1. The high symmetr y also enforces much more cooperative tunneling motions, and the bifurcation rearrangement has not been obser ved. Rather, each v ibration-rot ation line is split into a doublet in a complicated tunneling process connecting only t wo degenerate minima on the tetramer IPS (49, 50), probably involv ing a second-order saddle point (Fig. 9).
The pent amer continues this str uctural evolution, being ver y similar to the trimer in both str ucture and dynamics (Fig. 10) (20, 22, 51, 52). Both torsional (f lipping) and bifurcation tunneling are obser ved, connecting 320 degenerate minima on the IPS, but the time scale of both tunneling motions is slower than in the trimer. In contrast to the trimer, splittings due to bifurcation tunneling have been obser ved only for (H2O)5 and not (D2O)5, due to both the stronger H-bond and stronger coupling of f lipping and ring puckering motion in the latter (52, 53). This coupling also requires heavy atom motion for the torsional motions and results in a much denser torsional manifold and a large number of dipole-allowed transitions at low f requencies (54). Many such transitions have been measured for the pent amer (Fig. 11), and the characterization of this torsional manifold is nearing completion (20, 22, 51, 55, 56).
The H-bond in the pentamer is nearly linear and the OOO distance of 2.76 Å is close to the value found for liquid water and especially ice, as the desired tetrahedral hydrogen bonding geometr y of the monomers is ver y nearly realized. Moreover, molecular dynamics simulations have shown that five-membered rings are a dominant topology in liquid water, and pentamer-like patterns have Fig. 8. The water tetramer has a highly symmetric homodromic S4 equilibrium structure resulting in oblate symmetric top spectra with no vibrational averaging required. The symmetric structure requires highly concerted tunneling motions and results in a signicantly more rigid structure than for the water trimer. The effect of many-body forces reduces the vibrationally averaged OOO distance from that of the trimer to 2.79 Å (2.74-Å ab initio equilibrium value) (105). The hydrogen bond is only 12° from linearity and the structure is very nearly planar.
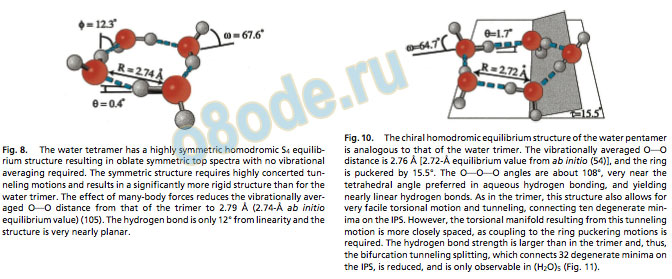
Fig. 9. The high symmetry of the tetramer requires highly concerted tunneling motions and limits the number of degenerate minima that can be connected on the IPS via feasible tunneling motions to two. The tunneling pathway connects the udud (up-down-up-down) structure with the dudu (down-up-down-up) one. Despite the small number of minima involved (trimer and pentamer 48 and 320 minima, respectively), the details of the tunneling pathway have been unclear. The observation of the large increase in tunneling splitting on exciting the 137.8 cm1 eg torsional vibration together with the analysis of the nuclear displacements derived by theory from this vibration suggests a complicated pathway involving sequential torsional motions of the free hydrogendeuterium atoms and tunneling via secondorder saddlepoints (49).
Fig. 10. The chiral homodromic equilibrium structure of the water pentamer is analogous to that of the water trimer. The vibrationally averaged OOO distance is 2.76 Å [2.72-Å equilibrium value from ab initio (54)], and the ring is puckered by 15.5°. The OOOOO angles are about 108°, very near the tetrahedral angle preferred in aqueous hydrogen bonding, and yielding nearly linear hydrogen bonds. As in the trimer, this structure also allows for very facile torsional motion and tunneling, connecting ten degenerate minima on the IPS. However, the torsional manifold resulting from this tunneling motion is more closely spaced, as coupling to the ring puckering motions is required. The hydrogen bond strength is larger than in the trimer and, thus, the bifurcation tunneling splitting, which connects 32 degenerate minima on the IPS, is reduced, and is only observable in (H2O)5 (Fig. 11).
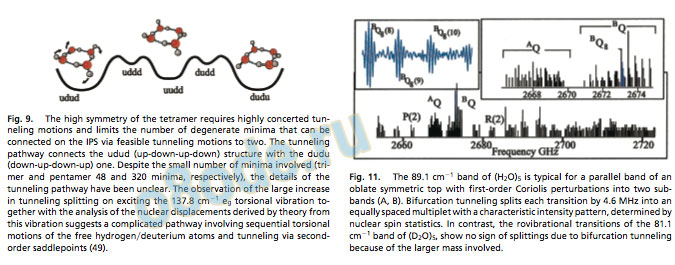
Fig. 11. The 89.1 cm1 band of (H2O)5 is typical for a parallel band of an oblate symmetric top with rst-order Coriolis perturbations into two subbands (A, B). Bifurcation tunneling splits each transition by 4.6 MHz into an equally spaced multiplet with a characteristic intensity pattern, determined by nuclear spin statistics. In contrast, the rovibrational transitions of the 81.1 cm1 band of (D2O)5, show no sign of splittings due to bifurcation tunneling because of the larger mass involved. been shown to be important in solvation of hydrophobic solutes and in the structures of clathrate hydrates (95).

The hexamer represents the transition of the H-bond net work f rom t wo-dimensional to three-dimensional in its most st able arrangement (Fig. 12). Here four monomers become triply H-bonded, whereas the t wo apical monomers remain doubly bonded in a nearly oct ahedral cage str ucture. These latter monomers engage in a cooperative t ype of bifurcation rearrangement, again enforced by the symmetr y of the hydrogen bond net work, and experiment ally, tunneling bet ween only t wo degenerate minima on the IPS is obser ved. It is not able that the most st able str ucture of the water hexamer deter mined in the gas phase resembles the basic unit in ice VI. Naut a and Miller (57) recently deter mined a cyclic str ucture of the hexamer in liquid helium droplets, analogous to those of the smaller clusters.
Interestingly, this str ucture closely resembles the six membered ring for ms ex isting in cr yst alline ice for ms of water.
Although high-resolution experiments have not yet been successful for clusters larger than the hexamer (H2O)n, clusters with n 7, 8, 9, 10 have been obser ved in low-resolution IR depletion experiments of size-selected clusters (58 – 60). The str uctures of these clusters were deter mined by comparing the experiment al v ibrational f requencies with the results of ab initio calculations for various str uctures. This analysis suggested the ex istence of both the D2d and S4 str uctures of the oct amer, both of which correspond to st acked tetramer rings. Two hept amer str uctures derived f rom the S4 oct amer str ucture by remov ing one of the monomers also were deter mined, as well as a nonamer str ucture, expanding the D2d cube str ucture of the oct amer, which is composed of pent amer and tetramer units, and a decamer str ucture resembling the D2d oct amer str ucture with the t wo additional water molecules inserted at opposite edges. Zwier and coworkers’ (61, 62) resonant t wo-photon ionization, UV hole-burning, and resonant ion-dip IR spectroscopy studies also have suggested the ex istence of the t wo isomers of the oct amer att ached to benzene, which acts as a chromophore.
Similarly, the str ucture of the water nonamer att ached to a benzene chromophore was proposed to consist of an expanded oct amer D2d str ucture, whereas the ex istence of additional nonamer str uctures based on the S4 oct amer str ucture could not be deter mined definitively (63).
Toward a Universal Water Force Field from VRT Spectra Theoretical calculations have clearly est ablished the rapid convergence of the liquid water force field in ter ms of N-body interactions. Moreover, the leading nonpair wise additive ter m has been shown to be the relatively simple polarization (induction) interaction (64). It is therefore apparent that the essential infor mation needed to deduce a quantit atively accurate liquid water force field can be extracted f rom appropriately det ailed measurements of small water clusters, particularly dimer and trimer. In contrast to the results of water cluster studies in bulk env ironments, FIR VRT spectroscopy has been shown to prov ide such a probe (65), being exquisitely sensitive to the det ailed topolog y of the cluster potential energ y sur face. Extensive VRT dat a sets now ex ist for several isotopomers of the dimer (66, 67) and trimer (25–27, 42, 46), encompassing all three t ypes (torsion, translation, libration) of inter molecular v ibrations of the trimer, and excluding only librations in the dimer (66, 67), whereas somewhat less dat a ex ist for the water tetramer, pent amer, and hexamer. Hence, given the requisite theoretical methods for computing cluster VRT spectra f rom global potential sur faces, we now have the capabilit y to actually constr uct a rigorously accurate force field for liquid water f rom the spectra of these small clusters.
The first step in our scheme to accomplish this goal is to rigorously deter mine the water dimer potential energ y sur face by explicitly fitting the VRT dat a to a det ailed and physically sound potential model. This dimer potential sur face will accurately describe not only the dominant pair wise interactions that occur in the liquid, but if it properly includes both electric multipoles and polarizibilit y of the water molecule, then it will also correctly describe the leading nonadditive ter ms, namely N-body induction. Hence, an approx imate potential sur face of the trimer can be constr ucted by appropriate summation of the polarizable dimer potential (treating the induction by iteration or matrix inversion). The interactions not properly described by this potential [three-body exchange and the much smaller (64) three-body dispersion] then can be quantified by comparing VRT spectra of the trimer with those computed f rom the potential sur face. This process can be extended and refined by successively addressing the larger clusters (tetramer, pent amer, and hexamer) in the same way. We suggest that a potential that rigorously describes the VRT spectra of the trimer will already accurately reproduce the measured properties of liquid water over large ranges of conditions, thereby essentially prov iding the long-sought universal water force field.
This first step outlined above (deter mination of the dimer potential) has now been accomplished. A key development in this process was the Split Wigner Pseudospectral method (68) and its implement ation for the water dimer (69, 70). This theoretical advance per mitted the accurate comput ation of dimer eigenst ates f rom van der Avoird’s rigorously derived body-fixed six-dimensional scattering Hamiltonian (71) and a suit able global potential sur face with the ver y high ef ficiency and economy required for incorporation of this procedure into a regression routine. Two water dimer potential sur faces of spectroscopic accuracy have now been published. Fellers et al . (38) fit the dimer VRT dat a to Millot and Stone’s ASP-W potential (72), the most det ailed dimer sur face available, and van der Avoird and colleagues (39, 73, 74) ‘‘tuned’’ the ab initio symmetr y adapted perturbation theor y (SAP T) sur face of Mas and Szalewicz (7) to reproduce these same dat a. The qualit y of these t wo potential sur faces is comparable, as judged by their respective abilities to reproduce the VRT dat a and the temperature dependence of the second v irial coef ficients. Both are far more accurate than any of the many water dimer potentials prev iously available (69, 70). Perhaps their most not able feature is the significantly reduced dimer binding energ y (4.85–5.00 kcalmol), in accord with the latest ab initio results (6, 7).
Perhaps surprisingly, we now recognize that the key ingredient for constr ucting a rigorously accurate liquid water force field is actually this dimer potential sur face. Accordingly, we must seek to obt ain the ‘‘per fect’’ dimer potential. Although the t wo new for ms obt ained f rom VRT dat a are cert ainly dramatic improveFig. 12. The water hexamer has been determined to have a cage structure with the oxygens forming a distorted octahedron. The two apical water monomers are single donors and acceptors, whereas two of the other water monomers act as single donors, double acceptors and the remaining two as double donors, single acceptors. Bifurcation tunneling exchanges the free and bound hydrogens of the two apical water monomers, connecting four degenerate minima on the IPS. Calculations indicate that this cage form is the lowest of ve low energy structures (21). A cyclic hexamer form, similar to that of the pentamer, recently has been identied in a liquid He droplet environment (57). ments, they both have f laws. The VRT(ASP-W) sur face is weakest in its description of the acceptor switching tunneling motion, yielding a trimer f lipping barrier that is too high. The symmetr y adapted perturbation theor y (SAP T) potential is not explicitly polarizable, and therefore cannot be used in its present for m to constr uct potentials for either larger clusters or bulk water. Both potentials are constr ucted with ‘‘f rozen monomers,’’ and thus do not produce the slight elongation of the covalent OOH bond that is known to occur in the donor of the H-bond. The relaxation of the monomer rigidit y constraint may be necessar y to improve these features. However, this necessit ates rigorously solv ing a 12-dimensional v ibrational dynamics Hamiltonian, something not considered even remotely possible until ver y recently.
Leforestier et al . (C. Leforestier, N. Goldman, C. Keoshian, L. B. Braly, and R.J.S., unpublished work) recently per for med a least-squares fit of H2O dimer VRT dat a to a 12-dimensional potential, which uses the H2O monomer potential recently developed by Polyanski et al . (76) to describe the covalent bond v ibrations, and a modified Matsuoka Clementi Yoshimine (MCY) potential for m of Clementi and coworkers (77) for t he i nt er mol ecul ar i nt er act i ons . The ei gens t at es of t he 12-dimensional potential were computed by the Split Wegner Pseudospectral (SWPS) method, but incorporating an adiabatic separation bet ween the covalent and inter molecular motions. Interestingly, this ver y simple MCY potential (11 f ree parameters) fits the VRT dat a quite well, but only when the intramolecular nonrigidit y is included (but with no additional f ree parameters); the modified MCY potential per for med rather badly when only six-dimensional dynamics (rigid monomers) were calculated (69, 70, 78).
The BerkeleyNijmegen collaboration has achieved a complete characterization of the trimer VRT st ates in the torsional (pseudorot ational) manifold for both H2O and D2O isotopes (42, 46), first treated theoretically by Schu¨tz et al . (79). Van der Avoird et al . (80) have derived a rigorous body-fixed Hamiltonian for these motions, treating the three torsional motions explicitly (fully coupled) and the librational (bifurcation) motions perturbatively, while f reezing the translational v ibrations. The Berkeley group (42, 46) has accomplished a global fit of all of the torsional VRT dat a to this Hamiltonian. Groenenboom et al . (39) have subsequently used these st ates to check the ‘‘tuning’’ of their symmetr y adapted perturbation theor y (SAP T)-5st potential, finding an impressive level of agreement (39). Keutsch et al . have ver y recently characterized both the translational (26) and librational (27) v ibrations in the trimer by VRT spectroscopy, and Sabo et al . (81) have developed a four-dimensional trimer model incorporating the ef fects of the symmetric translational mode on the torsional st ates. Hence, the st age is set for carr ying out the refinement of the pair potential and the rigorous deter mination of the three-body corrections, pending some further development of the requisite theoretical for malism (to describe the coupling of translation, torsion, and libration in the rot ating f rame—another dif ficult 12-dimensional dynamics problem).
Dynamics of the Hydrogen Bond in Water Clusters
Although the deter mination of an accurate potential for liquid water has thus far been the main goal of the FIR-VRT water cluster studies, we recently have sought to exploit the molecular det ails of str uctures and hydrogen bond dynamics revealed in our VRT spectroscopy experiments to elucidate specific aspects of these dynamics occurring in the liquid (21, 49, 51, 55, 82). The hydrogen bond net work and its dynamics deter mine the unique properties of liquid water, and many dif ferent experiments have addressed these in ter ms of the underlying inter molecular motions (83–91). In contrast to the VRT experiments, these bulk experiments were either insensitive to the microscopic det ails or required extensive interpret ation (92). In conjunction with interpret ation by theoretical models, the experiment al results have suggested that both the translational (hydrogen bond stretch v ibration centered at 180 cm1 in H2O) and the librational motions (hindered rot ational v ibration about 300 –1,000 cm1 H2O) are directly involved in most dynamical processes (5, 85, 86, 89, 92–96).
The f ree hydrogens in small water clusters—the main distinction bet ween clusters and the bulk—are predicted not to inf luence these t wo import ant inter molecular motions (translation and libration) significantly (ref. 97 and A. Luzar, personal communication). Although water clusters are cert ainly not import ant as isolated constituents of liquid water and clearly cannot act as models of long time dynamics (e.g., dif fusion), we have investigated by using water clusters to unravel the det ails of hydrogen bond dynamics on ver y short time scales, specifically the hydrogen bond breaking dynamics (41). Chandler and Luzar (5, 92) have studied this aspect of the liquid dynamics v ia computer simulations, and their results imply that these dynamics are primarily local and do not var y significantly with the hydrogen bond order in the liquid. Their studies, in conjunction with the above experiments, also suggest that librational motions play the central role in liquid-st ate dynamics because they are the dominant motion for the initial breaking of hydrogen bonds in the extended net work. Whereas translational motions themselves do not lead to significant bond breaking, they can indirectly facilit ate the breaking by weakening the hydrogen bond (5, 91, 92, 95, 99). The interpret ation of recent dielectric relaxation measurements has even suggested that water molecules making only t wo hydrogen bonds might be of special import ance for bulk dynamics (88). These results therefore suggest that water clusters can indeed prov ide a paradigm for elucidating the molecular det ails of specific local processes contributing to the liquid-st ate dynamics, namely the hydrogen bond breaking, despite the obv ious disparities.
Water cluster VRT experiments do not cont ain dynamical infor mation per se, as they measure transitions bet ween st ationar y st ates. However, the magnitude of the tunneling splittings obser ved for a specific v ibrational st ate characterize the feasible hydrogen bond rearrangements in the cluster. It is straightforward to extract a time scale for a given tunneling motion f rom the experiment al splittings (100, 101), and thus the time scale for the hydrogen bond dynamics associated with a tunneling pathway can be deter mined. This time scale calculation allows a direct study of the ef fect of exciting specific inter molecular motions (e.g., translation and libration) on the dynamics for various cluster sizes.
The bifurcation pathway (Fig. 6b) is uniquely suited for the study of the dynamics of the hydrogen bond in small water clusters, as it has been obser ved for the dimer, trimer, pent amer, and hexamer (49, 51), and corresponds to the lowest energ y pathway for breaking and making a hydrogen bond, precisely the aspect of the liquid-st ate dynamics we are interested in. Further more, the potential barrier for the bifurcation pathway is similar for all water clusters studied so far and it is a local process (49, 51), hence we can use this specific tunneling process as a probe of the hydrogen bond breaking dynamics and investigate the ef fect of both cluster size and excit ation of various intermolecular v ibrations on these bifurcation dynamics. From the experiment ally deter mined magnitude of the bifurcation tunneling splitting for a given v ibrational st ate, we can extract the time scale for breaking and making a hydrogen bond—i.e., the hydrogen bond lifetime (H) of that st ate. Presently, the water trimer is the only water cluster for which all classes of inter molecular v ibrations have been obser ved, allowing the first study of inter molecular v ibrational mode selectiv it y on the hydrogen bond lifetime, and the deter mination of the dominant inter molecular hydrogen bond breaking motion.
From a v ibrational ground st ate splitting of about 0.0033 cm1 the hydrogen bond lifetime of the ground st ate was deter mined to be H(GS) 1–2 ns for (H2O)3 (101). The ver y small variation of the magnitude of the tunneling splitting among st ates examined in the torsional manifold confir ms that the hydrogen bond lifetime does not change significantly upon excit ation of torsional v ibrations, H(torsion) 1–2 ns for (H2O)3 (101). The first obser ved translational v ibration of a water cluster, the 142.8 cm1 (D2O)3 band (Fig. 7), showed no ev idence of bifurcation tunneling splittings within the experiment al uncert aint y (about 2 MHz) (26). Therefore, the magnitude of these tunneling splitting and, thus, the hydrogen bond lifetime for the excited st ate has to be nearly identical upon exciting the translational v ibration, H(translation) H(GS) 1–2 ns for (H2O)3. Our recent study of the librational band region revealed three parallel bands of (H2O)3 at 517.2, 523.9, and 525.3 cm1 (Fig. 7), which are located close to the center of the librational band of liquid H2O and are assigned to the out-of-plane libration (27). The splittings for the excited st ate of the libration are so large that the three indiv idual bands obser ved within 8 cm1 correspond to the tunneling components, revealing that the bifurcation splittings are nearly 3 orders of magnitude larger than for the v ibrational ground st ate. Although the calculation of the hydrogen bond lifetime is more complicated for the excited st ate of the out-ofplane libration as the high barrier limit for the tunneling pathway is no longer valid, we can extract a hydrogen bond lifetime of H(libration) 1– 6 ps.
This time scale is strikingly similar to the accepted average hydrogen bond lifetime found in liquid water (1 ps), and the time scales of a number of import ant dynamical processes in bulk phases of water, (attributed to single molecule reorient ation) e.g., dielectric relaxation (D 8 –9 ps, D2 1 ps) (93), reorient ation relaxation (1 13 ps, 2 0.7 ps) (90) and proton mobilit y (1 ps) (93). Whereas the molecular det ails of the tunneling motions and v ibrations we obser ve in small water clusters are well understood (43, 44, 102), none of the experiments used for measuring these bulk time scales are sensitive to the microscopic det ails, and accordingly any molecular interpret ation of these results on the bulk is necessarily strongly model-dependent. The value of the VRT results is that they clearly demonstrate the dramatic ef fect of exciting specific inter molecular motions on the hydrogen bond breaking rate, with the librations clearly being the dominant inter molecular hydrogen bond breaking motion. Therefore, rather than the perhaps coincident al similarities of H(libration) with those of the bulk relaxation processes, the most import ant result of our study is that we have confir med the same dependence of the hydrogen bond breaking dynamics on inter molecular motions in the water trimer as postulated in theoretical studies of liquid water. Specifically, we obser ve a dramatic increase (1,000) in the rate of hydrogen bond breaking compared with that in the ground st ate of the water trimer upon excit ation of a single quantum in the librational mode, no change of H upon single quantum excit ation of a translational mode, and an insignificant change of H on excit ation of the torsional v ibrations. Hence, libration is the dominant vehicle for breaking and making the hydrogen bond, just as postulated to be the case for liquid water. This work was supported mainly by the Experiment al Physical Chemistr y Program of the National Science Foundation. The Berkeley cav it y ringdown laser absorption spectrometr y ef fort also was supported by the Chemical Dynamics Program of the Air Force Of fice of Scientific Research.
1. Stillinger, F. H. (1980) Science 209, 451– 457.
2. Chen, B., Xing, J. & Siepmann, J. I. (2000) J. Phys. Chem. 104, 2391–2401.
3. Makkonen, L. (1997) J. Phys. Chem. 101, 6196 – 6200.
4. Harrington, S., Zhang, R., Poole, P. H., Sciortino, F. & St anley, H. E. (1997) Phys. Rev. Lett . 78, 2409 –2412.
5. Luzar, A. & Chandler, D. (1996) Phys. Rev. Lett . 76, 928 –931.
6. Stone, A. J. (1996) The Theor y of Inter molecular Forces (Oxford Univ. Press, Oxford).
7. Mas, E. M. & Szalewicz, K. (1996) J. Chem. Phys. 104, 7606 –7614.
8. Silvestrelli, P. L. & Parrinello, M. (1999) J. Chem. Phys. 111, 3572–3580.
9. Busarow, K. L., Cohen, R. C., Blake, G. A., Laughlin, K. B., Lee, Y. T. & Saykally, R. J. (1989) J. Chem. Phys. 90, 3937–3943.
10. Dyke, T. R., Mack, K. M. & Muenter, J. S. (1977) J. Chem. Phys. 66, 498 –510.
11. Fraser, G. T. (1991) Int . Rev. Phys. Chem. 10, 189 –206.
12. Zwart, E., Ter meulen, J. J., Meerts, W. L. & Coudert, L. H. (1991) J. Mol . Spectrosc. 147, 27–39.
13. Pugliano, N. & Saykally, R. J. (1992) Science 257, 1937–1940.
14. Blake, G. A., Laughlin, K. B., Cohen, R. C., Busarow, K. L., Gwo, D. H., Schmuttenmaer, C. A., Steyert, D. W. & Saykally, R. J. (1991) Rev. Sci . Instr. 62, 1693–1700.
15. Blake, G. A., Laughlin, K. B., Cohen, R. C., Busarow, K. L., Gwo, D. H., Schmuttenmaer, C. A., Steyert, D. W. & Saykally, R. J. (1991) Rev. Sci . Instr. 62, 1701–1716.
16. Liu, K., Fellers, R. S., Viant, M. R., McLaughlin, R. P., Brown, M. G. & Saykally, R. J. (1996) Rev. Sci . Instr. 67, 410 – 416.
17. Pugliano, N., Cr uzan, J. D., Loeser, J. G. & Saykally, R. J. (1993) J. Chem. Phys. 98, 6600 – 6617.
18. Liu, K., Elrod, M. J., Loeser, J. G., Cr uzan, J. D., Pugliano, N., Brown, M. G., Rzepiela, J. & Saykally, R. J. (1994) Faraday Discuss. Chem. Soc. 94, 35– 41.
19. Cr uzan, J. D., Braly, L. B., Liu, K., Brown, M. G., Loeser, J. G. & Saykally, R. J. (1996) Science 271, 59 – 62.
20. Liu, K., Brown, M. G., Cr uzan, J. D. & Saykally, R. J. (1996) Science 271, 62– 64.
21. Liu, K., Brown, M. G., Carter, C., Saykally, R. J., Gregor y, J. K. & Clar y, D. C. (1996) Nature (London) 381, 501–503.
22. Liu, K., Brown, M. G., Cr uzan, J. D. & Saykally, R. J. (1997) J. Phys. Chem. 101, 9011–9021.
23. Liu, K., Brown, M. G. & Saykally, R. J. (1997) J. Phys. Chem. 101, 8995–9010.
24. Cr uzan, J. D., Viant, M. R., Brown, M. G. & Saykally, R. J. (1997) J. Phys. Chem. 101, 9022–9031.
25. Viant, M. R., Cr uzan, J. D., Lucas, D. D., Brown, M. G., Liu, K. & Saykally, R. J. (1997) J. Phys. Chem. 101, 9032–9041.
26. Keutsch, F. N., Brown, M. G., Petersen, P. B., Saykally, R. J., Geleijns, M. & van der Avoird, A. (2000) J. Chem. Phys. 114, 3934 – 4004.
27. Keutsch, F. N., Fellers, R., Viant, M. R. & Saykally, R. J. (2000) J. Chem. Phys. 114, 4005– 4015.
28. van Thiel, M., Becker, E. D. & Pimentel, G. C. (1957) J. Chem. Phys. 27, 486 – 490.
29. Vernon, M. F., Lisy, J. M., Krajnov ich, D. J., Tramer, A., Hoi-Sing, K., Ron Shen, Y. & Lee, Y. T. (1982) Faraday Discuss. Chem. Soc. 73, 387–397.
30. Page, R. H., Frey, J. G., Shen, Y. R. & Lee, Y. T. (1984) Chem. Phys. Lett . 106, 373–376.
31. Coker, D. F., Miller, R. E. & Watts, R. O. (1985) J. Chem. Phys. 82, 3554 –3562.
32. Huang, Z. S. & Miller, R. E. (1989) J. Chem. Phys. 91, 6613– 6631.
33. Huang, Z. S. & Miller, R. E. (1988) J. Chem. Phys. 88, 8008 – 8009.
34. Frochtenicht, R., Kaloudis, M., Koch, M. & Huisken, F. (1996) J. Chem. Phys. 105, 6128 – 6140.
35. Paul, J. B., Provencal, R. A., Chapo, C., Roth, K., Casaes, R. & Saykally, R. J. (1999) J. Phys. Chem. 103, 2972–2974.
36. Paul, J. B., Provencal, R. A. & Saykally, R. J. (1998) J. Phys. Chem. 102, 3279 –3283.
37. Paul, J. B., Provencal, R. A., Chapo, C., Petterson, A. & Saykally, R. J. (1998) J. Chem. Phys. 109, 10201–10206.
38. Fellers, R. S., Leforestier, C., Braly, L. B. & Brown, M. G. (1999) Science 284, 945–948.
39. Groenenboom, G. C., Mas, E. M., Bukowski, R., Szalewicz, K., Wor mer, P. E. S. & van der Avoird, A. (2000) Phys. Rev. Lett . 84, 4072– 4075.
40. Paul, J. B., Collier, C. P., Saykally, R. J., Scherer, J. J. & O’Keefe, A. (1997) J. Phys. Chem. 101, 5211–5214.
41. Keutsch, F. N., Fellers, R. S., Brown, M. G., Viant, M. R., Petersen, P. B. & Saykally, R. J. (2001) J. Am. Chem. Soc. 123, 5938 –5941.
42. Viant, M. R., Brown, M. G., Cr uzan, J. D., Saykally, R. J., Geleijns, M. & van der Avoird, A. (1999) J. Chem. Phys. 110, 4369 – 4381.
43. Wales, D. J. (1993) J. Am. Chem. Soc. 115, 11180 –11190.
44. Walsh, T. R. & Wales, D. J. (1996) J. Chem. Soc. Faraday Trans. 92, 2505–2517.
45. Fowler, J. E. & Schaefer, H. F. (1995) J. Am. Chem. Soc. 117, 446 – 452.
46. Brown, M. G., Viant, M. R., McLaughlin, R. P., Keoshian, C. J., Michael, E., Cr uzan, J. D., Saykally, R. J., Geleijns, M. & van der Avoird, A. (1999) J. Chem. Phys. 111, 7789 –7800.
47. Keutsch, F. N., Kar yakin, E. N., Saykally, R. J. & van der Avoird, A. (2000) J. Chem. Phys. 114, 3988 –3933.
48. Cr uzan, J. D., Brown, M. G., Liu, K., Braly, L. B. & Saykally, R. J. (1996) J. Chem. Phys. 105, 6634 – 6644.
49. Brown, M. G., Keutsch, F. N., Braly, L. B. & Saykally, R. J. (1999) J. Chem. Phys. 111, 7801–7806.
50. Wales, D. J. & Walsh, T. R. (1997) J. Chem. Phys. 106, 7193–7207.
51. Brown, M. G., Keutsch, F. N. & Saykally, R. J. (1998) J. Chem. Phys. 109, 9645–9647.
52. Wales, D. J. & Walsh, T. R. (1996) J. Chem. Phys. 105, 6957– 6971.
53. Gregor y, J. K. & Clar y, D. C. (1996) J. Chem. Phys. 105, 6626 – 6633.
54. Graf, S., Mohr, W. & Leut wyler, S. (1999) J. Chem. Phys. 110, 7893–7908.
55. Liu, K., Cr uzan, J. D. & Saykally, R. J. (1996) Science 271, 929 –933.
56. Cr uzan, J. D., Viant, M. G., Brown, M. G., Lucas, D. D., Kun, L. & Saykally, R. J. (1998) Chem. Phys. Lett . 292, 667– 676.
57. Naut a, K. & Miller, R. E. (2000) Science 287, 293–295.
58. Sadlej, J., Buch, V., Kazimirski, J. K. & Buck, U. (1999) J. Phys. Chem. 103, 4933– 4947.
59. Br uder mann, J., Melzer, M., Buck, U., Kazimirski, J. K., Sadlej, J. & Buch, V. (1999) J. Chem. Phys. 110, 10649 –10652.
60. Buck, U., Ettischer, I., Melzer, M., Buch, V. & Sadlej, J. (1998) Phys. Rev. Lett . 80, 2578 –2581.
61. Gr uenloh, C. J., Carney, J. R., Hagemeister, F. C., Arrington, C. A., Zwier, T. S., Fredericks, S. Y., Wood, J. T., III & Jordan, K. D. (1998) J. Chem. Phys. 109, 6601– 6614.
62. Gr uenloh, C., Carney, J., Arrington, C., Zwier, T., Fredericks, S. & Jordan, K. (1997) Science 276, 1678 –1681.
63. Gr uenloh, C. J., Carney, J. R., Hagemeister, F. C., Zwier, T. S., Wood, J. T. & Jordan, K. D. (2000) J. Chem. Phys. 113, 2290 –2303.
64. Xantheas, S. S. (1994) J. Chem. Phys. 100, 7523–7534.
65. Saykally, R. J. & Blake, G. A. (1993) Science 259, 1570 –1575.
66. Braly, L. B., Cr uzan, J. D., Liu, K., Fellers, R. S. & Saykally, R. J. (2000) J. Chem. Phys. 112, 10293–10313.
67. Braly, L. B., Liu, K., Brown, M. G., Keutsch, F. N., Fellers, R. S. & Saykally, R. J. (2000) J. Chem. Phys. 112, 10314 –10326.
68. Leforestier, C. (1994) J. Chem. Phys. 101, 7357–7363.
69. Leforestier, C., Braly, L. B., Kun, L., Elrod, M. J. & Saykally, R. J. (1997) J. Chem. Phys. 106, 8527– 8544.
70. Fellers, R. S., Braly, L. B., Saykally, R. J. & Leforestier, C. (1999) J. Chem. Phys. 110, 6306 – 6318.
71. Brocks, G., van der Avoird, A., Sutclif fe, B. T. & Tennyson, J. (1983) Mol . Phys. 60, 1025–1043.
72. Millot, C. & Stone, A. J. (1992) Mol . Phys. 77, 439 – 462.
73. Mas, E. M., Bukowski, R., Szalewicz, K., Groenenboom, G. C., Wor mer, P. E. S. & van der Avoird, A. (2000) J. Chem. Phys. 113, 6687– 6701.
74. Groenenboom, G. C., Wor mer, P. E. S., van der Avoird, A., Mas, E. M., Bukowski, R. & Szalewicz, K. (2000) J. Chem. Phys. 113, 6702– 6715.
75. Xantheas, S. S. & Dunning, T. H., Jr. (1993) J. Chem. Phys. 99, 8774 – 8792.
76. Polyansky, O., Jensen, P. & Tennyson, J. (1996) J. Chem. Phys. 105, 6490 – 6497.
77. Matsuoka, O., Clementi, E. & Yoshimine, M. (1976) J. Chem. Phys. 64, 1351–1361.
78. Fellers, R. S. (1998) Ph.D. Thesis (Univ. of California, Berkeley).
79. Schutz, M., Burgi, T., Leut wyler, S. & Burgi, H. B. (1993) J. Chem. Phys. 99, 5228 –5238.
80. van der Avoird, A., Olthof, E. H. T. & Wor mer, P. E. S. (1996) J. Chem. Phys. 105, 8034 – 8050.
81. Sabo, D., Bacic, Z., Graf, S. & Leut wyler, S. (1999) J. Chem. Phys. 110, 5745–5757.
82. Liu, K., Loeser, J. G., Elrod, M. J., Host, B. C., Rzepiela, J. A., Pugliano, N. & Saykally, R. J. (1994) J. Am. Chem. Soc. 116, 3507–3512.
83. Draegert, D. A. & Williams, D. (1968) J. Chem. Phys. 48, 401– 407.
84. Ricci, M. A., Signorelli, G. & Mazzacurati, V. (1990) J. Phys. Cond. Matt . 2, SA183–SA187.
85. Teixeira, J., Bellissent-Funel, M.-C. & Chen, S.-H. (1990) J. Phys. Cond. Matt . 2, SA105–SA108.
86. Barthel, J., Bachhuber, K., Buchner, R. & Hetzenauer, H. (1990) Chem. Phys. Lett . 165, 369 –373.
87. Sastr y, S., St anley, H. E. & Sciortino, F. (1994) J. Chem. Phys. 100, 5361–5366.
88. Buchner, R., Barthel, J. & St abuer, J. (1999) Chem. Phys. Lett . 306, 57– 63.
89. Lang, M. J., Jordanides, X. J., Song, X. & Fleming, G. R. (1999) J. Chem. Phys. 110, 5884 –5892.
90. Woutersen, S., Emmerichs, U. & Bakker, H. J. (1997) Science 278, 658 – 660.
91. Bakker, H. J., Woutersen, S. & Nienjuys, H. K. (2000) Chem. Phys. 258, 233–245.
92. Luzar, A. & Chandler, D. (1996) Nature (London) 379, 55–57.
93. Agmon, N. (1996) J. Phys. Chem. 100, 1072–1080.
94. Chen, S.-H., Gallo, P., Sciortino, F. & Tart aglia, P. (1997) Phys. Rev. E 56, 4231– 4242.
95. Csajka, F. S. & Chandler, D. (1998) J. Chem. Phys. 109, 1125–1133.
96. Schmitt, U. W. & Voth, G. A. (1999) J. Chem. Phys. 111, 9361–9381.
97. Bosma, W. B., Fried, L. E. & Mukamel, S. (1993) J. Chem. Phys. 98, 4413– 4421.
98. Xantheas, S. S. & Dunning, T. H. (1993) J. Chem. Phys. 98, 8037– 8040.
99. Luzar, A. & Chandler, D. (1993) J. Chem. Phys. 98, 8160 – 8173.
100. Feynman, R. P., Leighton, R. B. & Sands, M. (1964) in The Feynman Lectures on Physics, eds. Feynman, R. P., Leighton, R. B. & Sands, M. (Addison– Wesley, Reading), pp. 8-12– 8-14.
101. Brown, M. G. (1999) Ph.D. Thesis (Univ. of California, Berkeley).
102. Olthof, E. H. T., van der Avoird, A., Wor mer, P. E. S., Liu, K. & Saykally, R. J. (1996) J. Chem. Phys. 105, 8051– 8063.
103. Suzuki, S. & Blake, G. A. (1994) Chem. Phys. Lett . 229, 499 –505.
104. Klopper, W., Schutz, M., Luthi, H. P. & Leut wyler, S. (1995) J. Chem. Phys. 103, 1085–1098.