The structure of water
© Ignat Ignatov, Oleg Mosin
Ignat Ignatov, DSc., Professor
Oleg Mosin, PhD
Contact E-mail: mosin-oleg@yandex.ru
Abstract
In this review it is reported about the research on the structure of intermolecular water cyclic associates (clusters) with general formula (Н2О)n and their charged ionic clusters [(Н2О)n]+ and [(Н2О)n]- by means of computer modeling and spectroscopy methods as 1Н-NMR, IR-spectroscopy, DNES, EXAFS-spectroscopy, X-Ray and neurons diffraction. The computer calculation of polyhedral nanoclusters (Н2О)n, where n = 3–20 are carried out. Based on this data the main structural mathematical models describing water structure (quasicrystalline, continious, fractal, fractal-clathrate) have been examined and some important physical characteristics were obtained. The average energy of hydrogen bonding (DEH…O) between Н2О molecules in the process of cluster formation was measured by the DNES method compiles –0,1067±0,0011 eV. It was also shown that water clusters formed from 2H2О were more stable, than those ones from Н2О due to isotopic effects of deuterium.
Keywords: hydrogen bond, water, structure, clusters.
Introduction
Water with its anomalous physical and chemical properties outranks all other natural substances on the Earth. The ancient philosophers considered water as the most important component of the matter. It performs a vital role in numerous biochemical and metabolic processes occurring in cells with participation of water, being a universal polar solvent for hydrophilic molecules having an affinity for water. Hydroxyl groups (-OH) in H2O molecule, are polar and therefore hydrophilic. Moreover water act as a reagent for a big number of chemical reactions (hydrolysis, oxidation-reduction reactions). In chemical processes water due to its high ionizing ability possesses strong amphoteric properties, and can act both as an acid and a base in reactions of chemical exchange.
Modern science has confirmed the role of water as a universal life sustaining component, which defines the structure and properties of inorganic and organic objects, consisted from water.. The recent development of molecular and structural-chemical concepts has enabled to clarify an explanation of ability of water molecules to form the short-lived hydrogen bonds with neighboring molecules and many other chemical substances to bond them into intermolecular associates. It has also become clear the role of bounded water in forming hydrated substances and their physicochemical conduct in aqueous solutions.
The great scientific and practical interest have the studies of a variety of specific supramolecular structures – cyclic water clusters described by general formula (H2O)n, which may be calculated and studied with the help of modern numerical computing methods. The clusters are also important for studying the structure of water and hydration phenomena at molecular level since they form the basic building blocks of the hydrated substances. This paper deals with the mathematical modeling of the water structure and water associates.
Results and Discussion
Nature of Hydrogen Bond in Liquids and Crystals
The peculiarities of chemical structure of Н2О molecule and weak bonds caused by electrostatic forces and donor-acceptor interaction between hydrogen and oxygen atoms in Н2О molecules create favorable conditions for formation of directed intermolecular hydrogen bonds (О–Н…О) with neighboring Н2О molecules, binding them into complex intermolecular associates which composition represented by general formula (H2O)n, where n can vary from 3 to 50 units [1]. The hydrogen bond – a form of association between the electronegative O oxyden atom and a H hydrogen atom, covalently bound to another electronegative O oxyden atom, is of vital importance in the chemistry of intermolecular interactions, based on weak electrostatic forces and donor-acceptor interactions with charge-transfer [2]. It results from interaction between electron-deficient H-atom of one Н2О molecule (hydrogen donor) and unshared electron pair of an electronegative O-atom (hydrogen acceptor) on the neighboring Н2О molecule; the structure of hydrogen bonding, therefore may be defined as О...Нd+–Оd-. As the result, the electron of the H-atom due to its relatively weak bond with the proton easily shifts to the electronegative O-atom. The O-atom with increased electronegativity becomes partly negatively charged – d-, while the Н-atom on the opposite side of the molecule becomes positively charged – d+, that leads to the polarization of Оd-–Нd+ of the covalent bond. In this process the proton becomes almost bared, and due to the electrostatic attraction forces are provided good conditions for convergence of O…O or О…Н atoms, leading to the chemical exchange of a proton in the reaction O–H...O « O...H–O. Although this interaction is essentially compensated by mutual repulsion of the molecules’ nuclei and electrons, the effect of the electrostatic forces and donor-acceptor interactions for Н2О molecule compiles 5–10 kcal per 1 mole of substance. It is explained by negligible small atomic radius of hydrogen and shortage of inner electron shells, which enables the neighboring H2O molecule to approach the hydrogen atom of another molecule at very close distance without experiencing any strong electrostatic repulsion.
The Н2О molecule has four sites of hydrogen bonding – two uncompensated positive charges at hydrogen atoms and two negative charges at the oxygen atom. Their mutual disposition is characterized by direction from the centre of regular tetrahedron (nucleus of oxygen atom) towards its vertexes. This allows to one Н2О molecule in condensed state to form up to 4 classical hydrogen bonds, two of which are donor bonds and the other two – acceptor ones (taking into consideration bifurkate (“two-forked”) hydrogen bond – 5) [3].
A hydrogen bond according to Bernal–Fowler rules [4] is characterized by the following parameters:
- an oxygen atom of each Н2О molecule is bound with four neighboring hydrogen atoms: by covalent bonding with two own hydrogen atoms, and by hydrogen bonding – with two neighboring hydrogen atoms (as in the crystalline structure of ice); each hydrogen atom in its turn is bound with oxygen atom of neighbour Н2О molecule;
- on the line of oxygen atom – there can be disposed only one proton Н+;
- c) the proton, which takes part in hydrogen bonding situated between two oxygen atoms, therefore has two equilibrium positions: it can be located near its oxygen atom at approximate distance of 1,0 Å, and near the neighboring oxygen atom at the distance of 1,7 Å as well, hence both a usual dimer HO–H...OH2 and an ion pair HO...H–OH2 may be formed during hydrogen bonding, i.e. the hydrogen bond is part electrostatic (~90 %) and part (~10 %) covalent [5]. The state of “a proton near the neighboring oxygen” is typical for the interphase boundary, i.e. near water-solid body or water–gas surfaces.
- the hydrogen bonding of a triad О–Н...О possess direction of the shorter O–H (®) covalent bond; the donor hydrogen bond tends to point directly at the acceptor electron pair (this direction means that the hydrogen atom being donated to the oxygen atom acceptor on another H2O molecule).
The most remarkable peculiarity of hydrogen bond, however, consists in its relatively low strength; it is 5–10 times weaker than chemical covalent bond [6]. In respect of energy hydrogen bond has an intermediate position between covalent bonds and intermolecular van der Waals forces, based on dipole-dipole interactions, holding the neutral molecules together in gasses or liquefied or solidified gasses. Hydrogen bonding produces interatomic distances shorter than the sum of van der Waals radii, and usually involves a limited number of interaction partners. These characteristics become more substantial when acceptors bind H-atoms from more electronegative donors. Hydrogen bonds hold H2O molecules on 15 % closer than if water was a simple liquid with van der Waals interactions. The hydrogen bond energy compiles 5–10 kcal/mole, while the energy of О–Н covalent bonds in H2O molecule – 109 kcal/mole [7]. The values of the average energy (∆EH...O) of hydrogen Н…О-bonds between H2O molecules make up 0,1067 ± 0,0011 eV [8]. With fluctuations of water temperature the average energy of hydrogen H...O-bonds in of water molecule associates changes. That is why hydrogen bonds in liquid state are relatively weak and unstable: it is thought that they can easily form and disappear as the result of temperature fluctuations [9].
Another key feature of hydrogen bond consists in its cooperativity coupling. Hydrogen bonding leads to the formation of the next hydrogen bond and redistribution of electrons, which in its turn promotes the formation of the following hydrogen bond, which length increasing with distance. Cooperative hydrogen bonding increases the O–H bond length, at the same time causing a reduction in the H…O and O…O distances. The protons held by individual H2O molecules may switch partners in an ordered manner within hydrogen networks [10]. As the result, aqueous solutions may undergo autoprotolysis, i.e. the H+ proton is released from Н2О molecule and then transferred and accepted by the neighboring Н2О molecule resulting in formation of hydronium ions as Н3О+, Н5О2+, Н7О3+, Н9О4+, etc. This leads to the fact, that water should be considered as associated liquid composed from a set of individual H2O molecules, linked together by hydrogen bonds and weak intermolecular van der Waals forces [11]. The simplest example of such associate can be a dimer of water:
(H2O)2 = H2O…HOH
The energy of the hydrogen bonding in the water dimer is ~0,2 eV (~5 kcal/mol), which is larger than the energy of thermal motion of the molecules at the temperature of 300 K. Hydrogen bonds are easily disintegrated and re-formed through an interval of time, which makes water structure quite unstable and changeable. This process leads to structural inhomogeneity of water characterizing it as an associated heterogeneous two-phase liquid with short-range ordering, i.e. with regularity in mutual positioning of atoms and molecules, which reoccurs only at distances comparable to distances between initial atoms, i.e. the first H2O layer. As it is known, a liquid in contrast to a solid body, is a dynamic system: its atoms, ions or molecules, keeping short-range order in mutual disposition, participate in thermal motion, the character of which is much more complicated than that of crystals. For example H2O molecules in liquid state under normal conditions (1 atm, 22 0С) are quiet mobile and can oscillate around their rotation axes, as well as to perform the random and directed shifts. This enabled for some individual molecules due to cooperative interactions to “jump up” from one place to another in an elementary volume of water. Random motion of molecules in liquids causes continuous changes in the distances between them. The statistical character of ordered arrangement of molecules in liquids results in fluctuations – continuously occurring deviations not only from average density, but from average orientation as well, because molecules in liquids are capable to form groups, in which a particular orientation prevails. Thus, the smaller these deviations are, the more frequently they occur in liquids.
The further important feature is that the hydrogen bonds are spatially oriented. As each Н2О molecule has four sites of hydrogen bond formation (two non-shared electron pairs at an oxygen atom and two uncompensated positive charges at a hydrogen atom), one Н2О molecule in a condensed state is capable to form hydrogen bonds with four Н2О molecules (two donor and two acceptor) (Figure 1), which results in forming a tetrahedron crystal structure clearly observed in ice crystals.
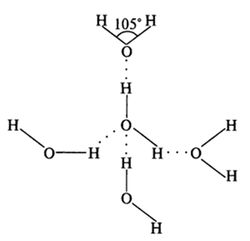
Figure 1. Hydrogen bonding between four individual Н2О molecules. It is shown the value of the angle between the covalent H–O–H bond in Н2О molecule.At present time 14 crystalline modifications of ice are known, each of them has its own structure and a character of disposition of hydrogen atoms (Table 1). Crystals of all ice modifications are made up from H2O molecules, linked by hydrogen bonds into a 3D carcass, consisting of individual tetrahedrons, formed by four H2O molecules (Figure 2). In the crystalline structure of natural ice Ih hydrogen bonds are oriented towards the tetrahedron apexes at strictly defined angles equal to 109°5’ (in liquid water this angle is 10405’). In ice structures Ic, VII and VIII this tetrahedron is nearly the same as a regular 4 triangular tetrahedron. In ice structures II, III, V and VI the tetrahedrons are noticeably distorted. In ice structures VI, VII and VIII two intercrossing systems of hydrogen bonds are distinguished. In the centre of the tetrahedron is located an oxygen atom, at each of the two vertices – H-atom, which electron take part in formation of covalent bond with an electron pair of O-atom. The rest two vertices of the tetrahedron are occupied by two pairs of non -shared electrons of O-atom not participating in formation of molecular bonds.
Table 1
Ice Crystal modifications and their physical characteristics
- Modification; Crystal structure; Hydrogen bond lengths, Å; Angles H–O–H in tetragonals, 0
- Ih; Hexagonal; 2,76; 109,5
- Ic; Cubic; 2,76; 109,5
- II; Trigonal; 2,75–2,84; 80,0–128,0
- III; Tetragonal; 2,76–2,8; 87,0–141,0
- IV; Rhombic; 2,78–2,88; 70,1–109,0
- V; Monoclinic; 2,76–2,87; 84,0–135,0
- VI; Tetragonal; 2,79–2,82; 76,0–128,0
- VII; Cubic; 2,86; 109,5
- VIII; Cubic; 2,86; 109,5
- IX; Tetragonal; 2,76–2,8; 87,0–141,0
- X; Cubic; 2,78; 109,5
- XI; Hexagonal; 4,50; 90,0
- XII; Tetragonal; 4,01; 90,0
- XIII; Monoclinic; 7,47; 90,0–109,7
- XIV; rhombic; 4,08; 90,0
Notes:
Ih – natural hexagonal ice; Ic – cubic ice.
The carcasses of hydrogen bonds allocate H2O molecules in form of a spatial hexagon network with internal hollow hexagonal channels. In the nodes of this network O-atoms are orderly organized (crystalline state), forming regular hexagons, while H-atoms have various positions along the bonds (amorphous state). When ice melts, its network structure is destroyed: H2O molecules begin to fall down into the network hollows, resulting in a denser structure of the liquid – this explains why water is heavier than ice. The hydrogen bonding explains other anomalies of water (anomality of temperature, presuure, density, viscosity, fluidity etc. According to theoretical calculations, at the melting of the ice breaks about 15 % of all hydrogen bonds [12]; by further heating to 40 0C breaks down about half of hydrogen bonds in water associates. In the water vapor hydrogen bonds are absent.
The main difference between the structure of ice and water is more diffuse arrangement of the atoms in the lattice and disturbance of long-range order. Thermal oscillations (fluctuations) lead to bending and breaking of hydrogen bonds. Those out of the equilibrium positions H2O molecules fall into the adjacent structural voids and for a time held up there, as cavities correspond to the relative minimum of potential energy. This leads to an increase in the coordination number, and the formation of lattice defects. The coordination number (the number of nearest neighbors) varies from 4,4 at t = 1,5 0С to 4,9 at t = 80 0С.
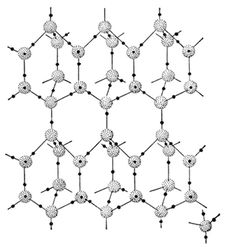
Figure 2. Hydrogen bonding in crystalline structure of natural ice Ih under the temperature -100C and pressure 1 atm. Grey balls – oxygen atoms, black balls – hydrogen atoms. On the right below shown the structural unit of crystalline ice structure.
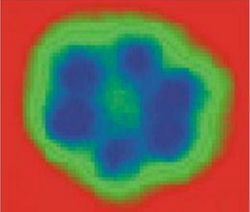
Figure 3. Image of hexamer nanocrystal of ice water (average size ~1 nm) by a scanning tunneling microscope after freezing water to 17 K on the hydrophobic metallic plates of Cu and Ag [13].
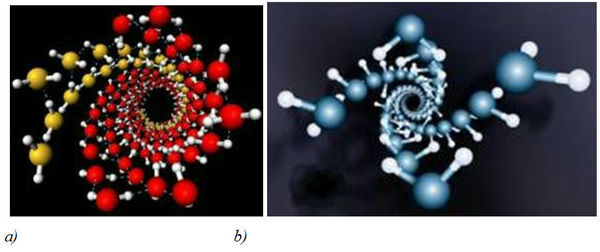
Figure 4. Structures of water crystals in carbon nanotubes according to computer simulations [14] (diameter of nanotubes: 1,35–1,90 nm; preassure: 10–40000 atm; temperature: -23 °C): a) – a general view of the crystal structure of water in nanotubes, b) – the inner wall of the structure of water.
Reports about evidence of existence of crystal structures in water have become more frequent in scientific literature nowadays [13]. As computer modeling showed, H2O molecules being placed in carbon nanotubes under high pressure and low temperatures formed crystalline nanostructures like DNA double helix [14]. In modeling experiment water got frozen inside carbon nanotubes with diameter 1,35–1,90 nm with pressure 10–40000 atm and temperature –23 °C. Hydrogen bonds in an ice crystal got distorted leading to the formation of a double-walled helix. The inner wall of this structure represents a four–fold twisted helix, while the outer consists of four double helixes, resembling a helix of DNA molecule (Figure 3). While being frozen at 17 К on hydrophobic surfaces of Cu, Ag and their salts, water became crystallized into two-dimensional ice hexamer nanocrystal, consisting of six attached together H2O molecules (Figure 4).
Structural Models of Water Regarding Hydrogen Bonding
There have been several groups of models, describing structure of liquids – microcrystalline, quasicrystalline, continious, fractal and fractal-clathrate models. The microcrystalline model of J. Bernal and P. Fowler suggests that water is a nonequilibrium 2-phase liquid containing groups of oriented molecules – microcrystals with several dozens or hundreds of molecules [15]. Within each microcrystal in liquid a solid body ordering (long-range order) is strictly kept. As water is denser than ice, it is assumed that its molecules are allocated in a different way than in ice: like the аtoms of silicon in mineral tridymite or in its more solid modification of quarz. The intermittent increase in water density from t = 0 °C to 3,98 °C and other anomalous properties of water was explained by the existence of tridymite component at low temperatures [16].
Quasicrystalline model by analogy with a quasicrystal, i.g. a structure that is ordered but not periodic [17], suggests that relative disposition of particles in liquids is nearly the same as in crystals; deviation from regularity increases with the distance from the initial H2O molecule; far apart at londer distances there is no regularity in the disposition of H2O molecules. Each H2O molecule is surrounded by the four neighbouring ones, which are arranged around it in quite the same way, as they are in an ice crystal. However, in the second layer there appear deviations from regularity rapidly increasing with distance from the initial H2O molecule. Studies of X-ray scattering in liquids consisting of polyatomic molecules, revealed not only some regular arrangement of H2O molecules, but consistent pattern in mutual orientation of the molecules [18]. This orientation becomes even more expressed for the polar molecules because of the hydrogen bonding effect.
Kinetic theory of liquids proposed by Y.I. Frenkel, also called a “jump-wait“ model, explains the structural properties of liquids by peculiarities of thermal motion of their molecules [19]. The thermal motion of H2O molecules is characterized by two parameters: a period of oscillation of H2O molecule around an equilibrium position and a period of “settled life”, i.e. period of oscillation around one particular equilibrium position. Average time of “settled life” of a H2O molecule, within which H2O molecules keep unchanged equilibrium orientation is called relaxation time t:
t = t0 x eW/RT, (1)
where t0 is an average period of oscillations of a H2O molecule around an equilibrium position (sec), W – a value of potential energy barrier, separating two neighboring equilibrium positions from each other (J), R – Boltzmann constant (J/К), T – absolute temperature (К).
According to calculations the relaxation time at room temperature makes up ~4,5.10-12 sec, while the period of one oscillation of H2O molecules – 10-12–10-13 sec. That is why each H2O molecule performs approximately 100 oscillations relative to the same equilibrium position before changing its place. Due to thermal fluctuations one H2O molecule within its “settled life” period of time oscillates around an equilibrium position, after then jumps up to new location and it continues to fluctuate up to the next jump. Through these abrupt movements of molecules in liquids occurs diffusion, which, in contrast to the continuous difusion in gases, called diffusion jump. With increase in temperature the period of “settled life” of H2O molecules in a temporary state of equilibrium is reduced that brings the structure of water closer to a gas, in which translational and rotational motions of H2O molecules prevail. Theoretical studies show that, along with the fluctuation of molecules surrounded by his neighbors and activation jumps in liquids occurs flowing movement of molecules along with their immediate environment. In other words, being in oscillating state, the molecules in the liquid displaced each time by a certain distance (less than the interatomic didtance), causing continuous diffusion. It is believed that in the liquefied inert gases and metals dominates continuous diffusion, while for associated liquids as water is more likely the jump diffusion mechanism. The thermal motion of H2O molecules leads to continuous changes in distances between them, which cause fluctuations – continual deviations not only from the average density, but from the average orientation of the molecules as well, because H2O molecules can form groups in which a certain orientation predominates. An attempt to change the water volume (even by small quantity) triggers the process of deformation of hydrogen bonds that fact may explain low water compressibility. Ice melting also causes weakening and deformation of hydrogen bonds, which makes water denser than ice. At the temperature 3,98 °С water acquires anomalous state, in which the quasicrystalline phase is maximally densified by filling up of ice carcass hollows with H2O molecules. Further increase in temperature and energy of thermal motion of H2O molecules leads to the gradual disintegration of associated water structures and to the partial rupture of hydrogen bonds with essential reduce of the “settled life” of each H2O molecule in water associates.
The continuous and “fractal” models consider water as a complex dynamic system with a hydrogen network, forming the empty cavities and non-bonded H2O molecules distributed within the network. The structure is based upon a dimensional carcass of individual H2O molecules, joined together into a multi-molecular associate similar to a clathrate having a configuration of a regular polyhedron. Stated geometrically, this model represents the packed spheres with varying degrees of packaging. Thus, the pentagonal packing of spheres, showed in Figure 5b, is denser, than the sphere packing model in Figure 5а (its density is 72 %). Analogous structure has clathrate hydrates (gas clathrates) – crystalline water-based solids physically resembling ice, in which small non polar gas molecules are plased inside cavities of hydrogen bonded H2O molecules.
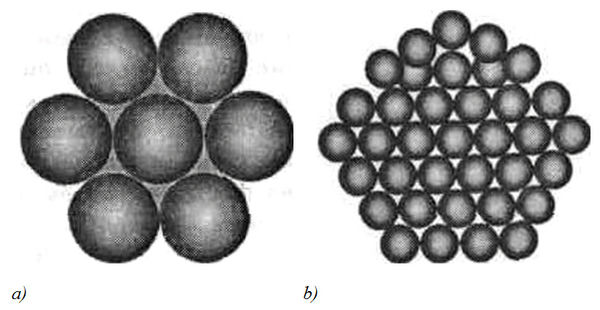
Figure 5. The sphere (a) and the pentagonal (b) packing of balls representing H2O molecules in clusters.
In 1957 S.Frank and W. Wen proposed a model, postulating arbitrary formation of cyclic associates in water, which presumably had random groups of water associates – the “flickering clusters” with general formula (Н2О)n, which are in a dynamic equilibrium with free H2O molecules [20]. The hydrogen bonds between H2O molecules are in dynamic equilibrium; they are constantly broken and re-formed in new configurations within a certain time interval; these processes are occurred cooperatively within short-living associated groups of H2O molecules (clusters), which life spans are estimated from 10-10 to 10-11 sec.
Water associates evidently may have polymer structure, because hydrogen bond is on 10 % partially covalent bond [21]. In 1990 G.А. Domrachev and D.А. Selivanovsky formulated a model of Н2О-polimers based on the existence of mechanochemical reactions of ionization and dissociation of water in aqueous solutions [22]. Water was thought as dynamically unstable quazi-polymer, composed of (Н2О)n blocks with partially covalent by 10 % hydrogen bonds, permitting at least to 10 % of Н2О molecules to comby in a sufficiently long-lived polymer associates. Similarly with mechanochemical reactions in polymers, in case of mechanical impact on water, the energy absorbed by water required for splitting up the Н–ОН bond, concentrates in a micro-scale area of the liquid water structure.
The splitting up reaction of the Н–ОН bond in water polymer associates is expressed by the following equation:
(Н2О)n(Н2О...H–|–OH) (Н2О)m + E = (Н2О)n+1 (H·) + (OH·) (Н2О)m, (2)
where Е – the energy of the Н–ОН bond, 460 кJ/mole; the dot denotes an unpaired electron.
Splitting up of the Н–ОН bond is accompanied by formation of new disordered bonds between “fragments” of the initial molecules, leading to the formation of fluctuation areas with different density fluctuations that can be observed in aqueous solutions.
Another interesting physical phenomenon was discovered by A. Antonov in 2005 [23]. It was established experimentally that at evaporation of water droplet the contact angle θ decreases discretely to zero, whereas the diameter of the droplet changes insignificantly. By measuring this angle within a regular time intervals a functional dependence f(θ) can be determined, which is designated by the spectrum of the water state. For practical purposes by registering the spectrum of water state it is possible to obtain information about the averaged energy of hydrogen bonds in an aqueous sample. For this purpose the model of W. Luck is used, which consider water as an associated liquid, consisted of О–Н…О–Н groups [24]. The major part of these groups is designated by the energy of hydrogen bonds (-E), while the others are free (E = 0). The energy distribution function f(E) is measured in electron-volts (eV-1) and may be varied under the influence of various external factors on water as temperature and pressure.
For calculation of the function f(E) experimental dependence between the water surface tension (θ) and the energy of hydrogen bonds (E) is established:
f(E) = b ´ f(θ)/[1 – (1 + b ´ E)2]1/2, (3)
where b = 14,33 eV-1
The energy of hydrogen bonds (Е) is measured in electron-volts (eV) and is designated by the spectrum of energy distribution. The water spectrum is characterized by a non-equilibrium process of water droplets evaporation, thus the term “non-equilibrium energy spectrum of water” (NES) is applied.
The difference ∆f(E) = f (samples of water) – f (control sample of water) is called the “differential non-equilibrium energy spectrum of water” (DNES). DNES is a measure of changes in the structure of water as a result of external influences. The cumulative effect of all other factors is the same for the control sample of water and the water sample, which is under the influence of this impact.
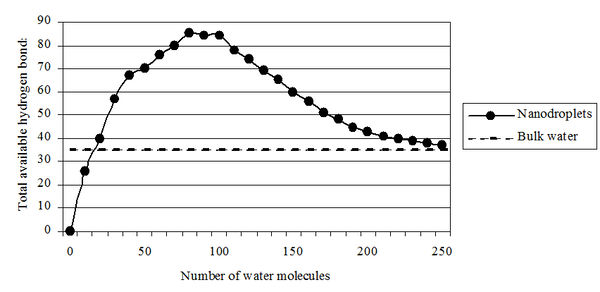
Figure 6. The total number of hydrogen bonds depending on the number of water molecules in clusters.
In 2005 R. Saykally (USA) calculated the possible number of hydrogen bonds and the stability of water clusters depending on the number of H2O molecules (Figure 6) [25]. It was also estimated the possible number of hydrogen bonds (100) depending on the number of H2O molecules (250) in clusters [26]. O. Loboda and O.V. Goncharuk provided data about the existence of icosahedral water clusters consisting of 280 H2O molecules with the average size up to 3 nm [27]. The ordering of water molecules into associates corresponds to a decrease in the entropy (randomness), or decrease in the overall Gibbs energy (G = DH – TDS). This means that the change in entalpy DH minus the change in entropy DS (multiplied by the absolute temperature T) is a negative value. These results are consistent with our data on research of DNES spectrum of water on which it may make conclusion about the number of H2O molecules in water clusters. DNES spectrum of water has energy ranges from –0,08 to –0,14 eV (Figure 7). The spectral range lies in the middle infrared range from 8 to 14 mm ("window" of the atmosphere transparency to electromagnetic radiation). Under these conditions, the relative stability of water clusters depends on external factors, primarily on the temperature.
It was shown that the H2O molecules change their position in clusters depending on the energy of intermolecular H…O hydrogen bonds. The values of the average energy (DEH…O) of hydrogen bonds between the H2O molecules in the formation of cluster associates with formula (H2O)n compile 0,1067±0,0011 eV. As the energy of hydrogen bonds between H2O molecules increases up to –0,14 eV, the cluster formation of water becomes “destructuring”. In this case, the energy redistribution between the individual H2O molecules occures (Figure 7).
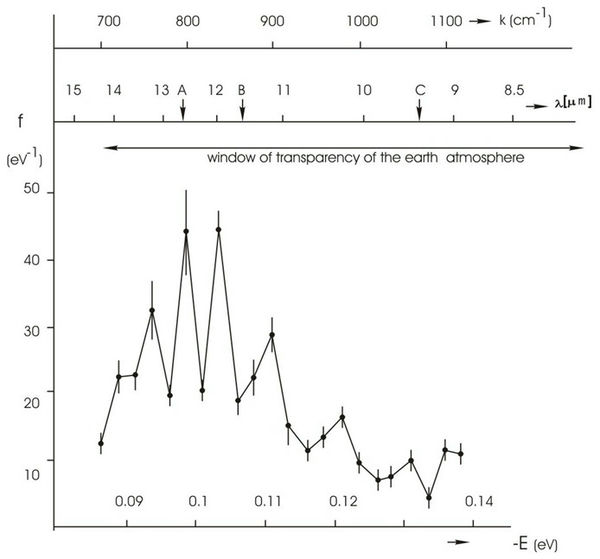
Figure 7. NES-spectrum of deionized water (chemical purity – 99,99%, pH – 6,5–7,5, total mineralization – 200 mg/l, electric conductivity – 10 mS/cm). On the horizontal axis shows the energy of the H...O hydrogen bonds in the associates – E (eV). The vertical axis – energy distribution function – f (eV-1). k – the wave number (cm-1); λ – wavelength (mm).
All these data indicate that the water is a complex associated non-equilibrium liquid consisting of associative groups containing according to the present data, from 3 to 20 individual H2O molecules [28]. Associates can be perceived as unstable groups (dimers, trimers, tetramers, pentamers, hexamers etc.) in which H2O molecules are linked by van der Waals forces, dipole-dipole and other charge-transfer interactions, including hydrogen bonding. At room temperature, the degree of association of H2O molecules may vary from 2 to 6 units. In 1993 K. Jordan (USA) [29] calculated the possible structural modifications of small water clusters consisting of six H2O molecules (Figure 8,a–c). Subsequently, it was shown that H2O molecules capable of hydrogen bonding by forming the structures representing topological 1D rings and 2D chains composed from numerous H2O molecules. Interpreting the experimental data, they are considered as pretty stable elements of the structure. According to computer simulations, clusters are able to interact with each other through the exposed protons on the outer surfaces of hydrogen bonds to form new clusters of more complex composition.
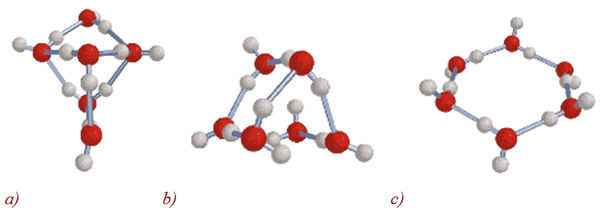
Figure 8. Calculation of small water cluster structures (a–c) with general formula (H2O)n, where n = 6 [29].
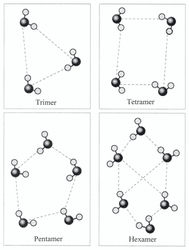
Figure 9. Cluster structure of a trimer, tetramer, pentamer and hexamer of water.In 2000 it was deciphered the structure of the trimmer water, and in 2003 – tetramer, pentamer and the water hexamer [30]. Structures of water clusters with formula (H2O)n, where n = 3–5, similar to the cage structure. Hexagonal structure with n = 6, consisting of six H2O molecules at the hexagon vertices, is less stable than the cage structure. In the hexagon structure four H2O molecules can be cross-linked by hydrogen bonds (Figure 9).
Quantum-chemical calculations of middle size clusters with the general formula (H2O)n, where n = 6–20, have shown that the most stable structures are formed by the interaction of tetrameric and pentameric structures [31]. Thus the structures of (H2O)n, where n = 8, 12, 16, and 20 are cubic, and structures (H2O)n where n = 10 and 15 – pentagons. Other structures with n = 9, 11, 13, 14, 17, 18 and 19 evidently have a mixed composition. Large tetrahedron clusters as (H2O)196, (H2O)224, (H2O)252 (Figure 10) composed from the smaller ones formed a vertex of a (H2O)14 tetrahedron are also described [32]
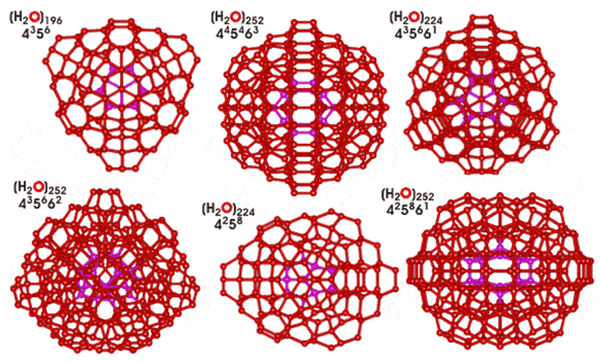
Figure 10. Tetrahedron water clusters (H2O)n with different symmetry (n = 196, 224, 252) [32].
It is reasonable that the structure of liquid water should be related to the structure of hexagonal ice, formed from H2O tetrahedrons, which exist under atmospheric pressure. In the computer simulation H2O tetrahedrons grouped together, to form a variety of 3D-spatial and 1D, 2D-planar structures, the most common of which is hexagonal structure where 6 H2O molecules (tetrahedrons) are combined into a ring. A similar type of structure is typical for ice Ih crystals. When ice melts, its hexagonal structure is destroyed, and a mixture of clusters consisting of tri-, tetra-, penta-, and hexamers of water and free H2O molecules is formed. Structural studies of these clusters are significantly impeded, since the water is perceived as a mixture of different clusters that are in dynamic equilibrium with each other.
In 1999 S.V. Zenin (Russia) calculated a cluster model based on a minimum ”quantum” of water [33], which is a 4 triangular tetrahedron composed of four 12 pentagonal dodecahedrons (Figure 11). The ”quantum” consisted of 57 H2O molecules interacting with each other at the expense of free hydrogen bonds exposed on the surface. Of 57 H2O molecules in the “quantum” 17 H2O molecules compose tetrahedral completely hydrophobic, i.e. saturated with four hydrogen bonds in the central carcass, and four dodecahedra on the surface of each there are 10 centers for the formation of hydrogen bond (O–H or O). 16 “quanta” form a bigger cluster structure consisted from 912 H2O molecules similar to a tetrahedron. Interaction is possible only in a cross position. Dotted lines are highlighted the simplest of five (fifth in central) and six quantum formations (Figure 11).
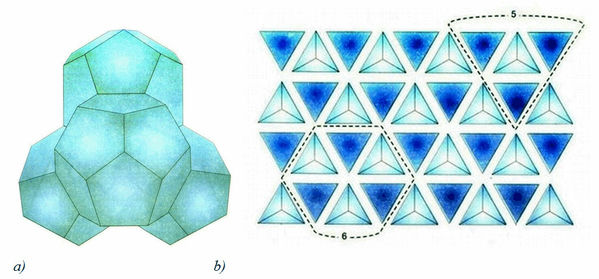
Figure 11. Model of water associate accordung to the model of S.V. Zenin [33]: a) – assosiate of 57 H2O molecules, tetrahedron of four dodecahedron (“quantum”); b) – bulk packaging of “quanta”
M. Chaplin (London South Bank University, UK) [34] calculated the water structure based on 20 triangular icosahedron (Figure 12). The structure is based on minimal tetrahedral water cluster, consisting of 14 H2O molecules. Arrangement of 20 of these 14-molecule structures forms an icosahedral network, consisting from 280 H2O molecules. Each 280-molecule in icosahedral contains several substructures with each H2O molecule involved in four hydrogen bonds; two as donor and two as acceptor. 13 overlapping icosahedra may form more large cluster (tricontahedron) consisting from 1820 H2O molecules, which has twice more H2O molecules than in the previous model.
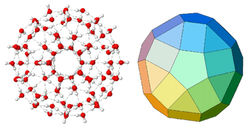
Figure 12. Icosahedron cluster based on 100 H2O molecules and the underlying structure according to the M. Chaplin’s model.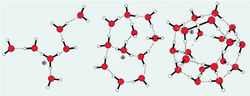
Figure 13. Formation of ionic clusters (H2O)20H3O+ or (H2O)21H+ with captured hydronium ion H3O+.The clusters, evidently, may be rather stable under a certain conditions, and can be obtained in the isolated state within a very short interval of time. There is also a reason to believe that the charged ions stabilize the clusters. Therefore, the clusters can be divided into positevely and negatively charged ionic clusters – [(H2O)n]+, [(H2O)n]-, and not having a charge – neutral clusters with general formula (H2O)n. Clusters, containing 20 individual H2O molecules and a proton in the form of hydronium ion H3O+ (“magic” number) form the most stable ionic clusters (H2O)20H3O+ or (H2O)21H+ (Figure 13) [35]. It is assumed that the stability of ionic clusters is due to the special clathrate structure in which 20 H2O molecules are formed 12 pentagonal dodecahedron, in which cavities is captured the H3O+ ion. It is occurred because of all the clusters only the dodecahedron has large cavities enough to accommodate a bulky H3O+ ion. Subsequently, due to cooperative interactions H3O+ is further able to move to the surface of the cluster and lose a proton H+ leading to the formation of hydronium ions like H5O2+, H7O3+, and H9O4+, fixed on the surface of the cluster. These data show the diversity of supposed water structures and the complexity of molecular interactions between the different water clusters, the nature of which we are only beginning to understand.
Methods of Study and Calculation of Water Clusters
Cluster structures in water calculated theoretically on computer were confirmed by 1H-NMR, IR, Raman, Compton scattering, EXAFS-spectroscopy and X-ray diffraction [36, 37]. Information obtained with using the modern detection methods corresponds to femtosecond time, i.e instantaneous dynamics of intermolecular interactions in the molecular scale. The presence of hydrogen bonding causes the noticable effect on vibrational and 1H-NMR spectra. In 1H-NMR the chemical shift of the proton involved in the hydrogen bonding shifts about 0,01 ppm reducing strength of hydrofen bonding while the temperature is raised. Increased extent of hydrogen bonding within clusters results in a similar effect; the higher chemical shifts with greater cooperativity, the shorter hydrogen bonded O-H…O distances. 1H peaks shift to greater ppm with increasing hydrogen bonding strength.
In IR-spectroscopy the characteristic vibration frequency bands containing hydrogen are reduced in spectra if hydrogen atom is included in the hydrogen bonding. Infrared absorption bands, such as OH-groups are much expanded when the hydrogen bond is formed, and their intensity increases. The main stretching band in liquid water is shifted to a lower fequency (v3 = 3480 cm-1 and v1 = 3270 cm-1), while the bending frequency (v2 = 1640 cm-1) increased by hydrogen bonding [38] Increased strength of hydrogen bonding shifts the stretch vibration to lower frequencies with greatly increased intensity in the infrared due to the increased dipoles. With raising the temperature the stretch vibrations shift to higher frequency, while the intramolecular vibrations shift to lower frequencies [39]. Hydrogen bond energy lies in the range of 2,3 kcal/mole for the N–H...O-bonds up to 7,0 kcal/mol for the bonds with hydrogen fluoride F–H...F. The strength of the hydrogen bonding depends on the cooperative/anticooperative character of the surrounding hydrogen bonds with the strongest hydrogen bonds giving the lowest vibrational frequencies.
In X-ray absorption spectroscopy (EXAFS-spectroscopy) X-ray radiation excites the electrons of the inner shell of an oxygen atom in H2O molecules and stipulates their transition onto unoccupied upper electronic levels in the molecules [40]. Probability of electron transitions and characteristics of the absorption contour depends mostly on the molecular environment. This allows by varying the energy of the X-rays to study the distribution of associations for HOH...OH2 bond judging on lengths and angles of the covalently bonded hydrogen atom in the molecule. EXAFS spectrum near the oxygen atom is also sensitive to hydrogen bonding. This method is used to obtain information about the molecular structure of water in the first coordination sphere. Since the time of excitation of electrons is much smaller than the vibrational motions in liquids, X-ray probe of the electronic structure provides information about the instantaneous changes of configurations of the water structure.
Diffraction techniques (X-ray and neutron diffraction) on liquid water allow calculate the function of density radial distribution (O or H) and the probability of detection of H2O molecules at a certain distance from a randomly chosen individual H2O molecule [41]. This allows detecting the irregularities in water by constructing the radial distribution function, i.e. the distance between the atoms of O, H, and O–H in H2O molecule and its nearest neighbors. Thus, the distribution of the distances between the oxygen atoms at a room temperature, gives three major peaks measured at 2,8; 4,5 and 6,7 Å. The first maximum corresponds to the distance to the nearest neighbor and its value is approximately equal to the length of the hydrogen bond. The second maximum is close to the average edge length of a tetrahedron, as H2O molecules in the crystalline structure of ice Ih arranged at the vertices of the tetrahedron allocated around the center of the molecule. The third peak, expressed very weakly, corresponds to the distance to the third and more distant neighboring H2O molecules on the hydrogen network. In 1970 I.S. Andrianov and I.Z. Fisher calculated the distance up to the eighth of the neighboring H2O molecule; the distance to the fifth the neighboring H2O molecule turned out to be 3 Å, and to the sixth molecule – 3,1 Å. This allowed draw conclusions about the geometry of hydrogen bonds and farther surroundings of H2O molecules.
Another method for structural studies – neutron diffraction is similar to X-ray diffraction. However, because the neutron scattering lengths vary slightly among different atoms, this method is limited in the case of the isomorphous substitution of hydrogen atoms in H2O molecule by deuterium (2H). In practice generally operate with a crystal whose molecular structure is approximately defined by other methods. Then, it is measured the intensity of the neutron diffraction of this crystal. From these results, the Fourier transform is carried out; the measured neutron intensity and phase are using for calculation. Then, on the resultant Fourier map hydrogen and deuterium atoms are represented with much greater atomic weight than on the electron density map, as the contribution of these atoms in neutron scattering is essentially big. On the resulting density map is determined the arrangement of hydrogen 1H (negative density) and deuterium 2H (positive density) atoms. A variation of the method consists in that the crystal of an ordinary protonated water (H2O) before measurements kept in 99,9 at.% of heavy water (2H2O). In this case the neutron diffraction can not only establish the localization of the hydrogen atoms, as well as to identify those protons that can be exchanged by deuterium, that is particularly important for the study of isotopic (1H–2H) exchange. Such information in some cases may help confirm the correctness of the water structure established by other methods.
Clusters formed of 2H2O are some more stable and resistant than those ones from H2O due to isotopic effects of deuterium caused by 2-fold increasing nuclear mass of deutereium (molecular mass of 2H2O is more by 11 % than that of H2O). The structure of 2H2O molecule is the same, as that of Н2O, with small distinction in values of lengths of covalent bonds. 2H2O crystals have the same structure as a conventional ice Ih, the difference in unit cell size is very insignificant (0,1 %). But they are heavy (0,982 g/cm3 at 0 0C over 0,917 g/cm3 for conventional ice). 2H2O boils at 101,44 0С, freezes at 3,82 0С, has density 1,105 g/cm3 at 20 0С, and the maximum density (1,106 g/cm3) occurs not at the 3,89 0C, as for H2O, but at 11,2 0C. The mobility of 2H3O+ ion is on 28,5 % lower than that of H3O+ ion and O2H- ion – 39,8 % lower than that of OH- ion, the constant of ionization of 2H2O is less than the constant of ionization of H2O, which means that 2H2O has a bit more hydrophobic properties than H2O. All these effects lead that the hydrogen bonds formed by deuterium atoms differ in strength and energy from ordinary hydrogen bonds (O–H length – 1,01 Å, O–2H length – 0,98 Å, 2H–O–2H angle – 1060). Commonly used molecular models use O–H lengths ~0,955 Å and 1,00 Å and H–O–H angles from ~105,50 to ~109,40. The substitution of 1H with 2H atom affects the stability and geometry of hydrogen bonds in apparently rather complex way and may, through the changes in the hydrogen bond zero-point vibrational energies, alter the conformational dynamics of hydrogen (deuterium)-bonded structures of associates. In general, isotopic effects stabilize hydrogen bond with participation of deuterium, resulting in somewhat greater stability of associates formed from 2H2O molecules [42].
As a result of experiments on quasi-elastic neutron scattering was measured the most important parameter – the coefficient of self-diffusion of water at different temperatures and pressures. To analyse the self-diffusion coefficient on quasi-elastic neutron scattering, it is necessary to know the character of moving of molecules. If they move in accordance with the “jump-wait“ model, then the “settled” life time (the time between jumps) of H2O molecule compiles 3,2 ps. The newest methods of femtosecond laser spectroscopy allow estimate the lifetime of the broken hydrogen bonds: a proton needs 200 fs to find a partner.
The studying the full details of the structure of associative elements in water can be made, considering all the parameters by computer simulation or numerical experiment. For this in a given space is chosen random ensemble of n H2O molecules and are optimal parameters – the energy of interatomic interactions, bond length, the arrangement of atoms and molecules, most consistent with the diffraction data. Data thus obtained are then extrapolated to the actual water structure, and further used to calculate thermodynamic parameters. Data obtained by computer experiments, show that the nature of the thermal motion of the molecules in the liquids corresponds on the whole to a vibration of the individual H2O molecules near the equilibrium centers, with occasional jumps up to the new position.
In conclusion it should be noted that comparative analysis of IR-spectra of H2O solutions and its deuterated analogues (2Н2О, H2НO) is of considerable interest for biophysical studies, because at changing of the atomic mass of hydrogen by deuterium atoms in H2O molecule their interaction will also change, although the electronic structure of the molecule and its ability to form H-bonds, however, remains the same. The local maximums in IR-spectra reflect vibrational-rotational transitions in the ground electronic state; the substitution with deuterium changes the vibrational-rotational transitions in H2O molecule, that is why it appear other local maximums in IR-spectra. In the water vapor state, the vibrations involve combinations of symmetric stretch (v1), asymmetric stretch (v3) and bending (v2) of the covalent bonds with absorption intensity (H2O) v1;v2;v3 = 2671; 1178,4; 2787,7 cm-1. For liquid water absorption bands are observed in other regions of the IR-spectrum, the most intense of which are located at 2100, cm-1 and 710-645 cm-1. For 2Н2О molecule these ratio compiles 2723,7; 1403,5 and 3707,5 cm-1, while for H2НО molecule – 2671,6; 1178,4 and 2787,7 cm-1. H2НO (50 mole% H2O + 50 mole% 2Н2О; ~50 % H2НO, ~25 % H2O, ~25 % 2Н2О) has local maxima in IR-spectra at 3415 cm-1, 2495 cm-1 1850 cm-1 and 1450 cm-1 assigned to OH- -stretch, O2Н- -stretch, as well as combination of bending and libration and H2НO bending respectively.
In the IR-spectrum of liquid water absorbance band considerably broadened and shifted relative to the corresponding bands in the spectrum of water vapor. Their position depends on the temperature [34]. The temperature dependence of individual spectral bands of liquid water is very complex [43]. Furthermore, the complexity of the IR-spectrum in the area of OH- stretching vibration can be explained by the existence of different types of H2O associations, manifestation of overtones and composite frequencies of OH- groups in the hydrogen bonds, and the tunneling effect of the proton (for relay mechanism) [44]. Such complexity makes it difficult to interpret the spectrum and partly explains the discrepancy in the literature available on this subject.
In liquid water and ice the IR-spectra are far more complex than those ones of the vapor due to vibrational overtones and combinations with librations (restricted rotations, i.g. rocking motions). These librations are due to the restrictions imposed by hydrogen bonding (minor L1 band at 395,5 cm-1; major L2 band at 686,3 cm-1; for liquid water at 0 0C, the absorbance of L1 increasing with increasing temperature, while L2 absorbance decreases but broadens with reduced wave number with increasing temperature [45]. The IR spectra of liquid water usually contain three absorbance bands, which can be identified on absorption band of the stretching vibration of OH- group; absorption band of the first overtone of the bending vibration of the molecule H2НO and absorption band of stretching vibration of O2Н- group. Hydroxyl group OH- is able to absorb much infrared radiation in the infrared region of the IR-spectrum. Because of its polarity, these groups typically react with each other or with other polar groups to form intra-and intermolecular hydrogen bonds. The hydroxyl groups, which are not involved in formation of hydrogen bonds usually produce the narrow bands in IR spectrum, while the associated groups – broad intense absorbance bands at lower frequencies. The magnitude of the frequency shift is determined by the strength of the hydrogen bond. Complication of the IR spectrum in the area of OH- stretching vibrations can be explained by the existence of different types of associations of H2O molecules, a manifestation of overtones and combination frequencies of OH- groups in hydrogen bonding, as well as the proton tunneling effect (on the relay mechanism).
Assignment of main absorption bands in the IR-spectrum of liquid water is given in the Table 2. The IR spectrum of H2O molecule was examined in detail from the microwave till the middle (4–17500 cm-1) visible region and the ultraviolet region – from 200 nm-1 to ionization limit at 98 nm-1 [46]. In the middle visible region at 4–7500 cm-1 are located rotational spectrum and the bands corresponding to the vibrational-rotational transitions in the ground electronic state. In the ultraviolet region (200 to 98 nm-1) are located bands corresponding to transitions from the excited electronic states close to the ionization limit in the electronic ground state. The intermediate region of the IR-spectrum – from 570 nm to 200 nm corresponds to transitions to higher vibrational levels of the ground electronic state.
Table 2
The assignment of main frequencies in IR-spectra of liquid water H2O and 2Н2О
- Main vibrations of liquid H2O and 2Н2О
- Vibration(s); H2O (t = 250 C); 2Н2О (t = 250 C)
- v, cm-1; E0, M-1 cm-1; v, cm-1; E0, M-1 cm-1
- Spinning ν1 + deformation ν 2; 780–1645; 21,65; 1210; 17,10
- Composite ν1 + ν2; 2150; 3,46; 1555; 1,88
- Valence symmetrical ν1, valence asymmetrical ν3, and overtone 2ν2; 3290–3450; 100,65; 2510; 69,70
At the transition from H2O monomers to H2O dimmer and H3O trimmer absorption maximum of valent stretching vibrations of the O-H bond is shifted toward lower frequencies (v3 = 3490 cm-1 and v1 = 3280 cm-1) and the bending frequency increased (v2 = 1644 cm-1) because of hydrogen bonding. The increased strength of hydrogen bonding typically shifts the stretch vibration to lower frequencies (red-shift) with greatly increased intensity in the infrared due to the increased dipoles. In contrast, for the deformation vibrations of the H-O-H, it is observed a shift towards higher frequencies. Absorption bands at 3546 and 3691 cm-1 were attributed to the stretching modes of the dimmer [(H2O)2]. These frequencies are significantly lower than the valence modes of ν1 and ν3 vibrations of isolated H2O molecules at 3657 and 3756 cm-1 respectively). The absorption band at 3250 cm-1 represents overtones of deformation vibrations. Among frequencies between 3250 and 3420 cm-1 is possible Fermi resonance (this resonance is a single substitution of intensity of one fluctuations by another fluctuation when they accidentally overlap each other). The absorption band at 1620 cm-1 is attributed to the deformation mode of the dimmer. This frequency is slightly higher than the deformation mode of the isolated H2O molecule (1596 cm-1). A shift of the band of deformation vibration of water in the direction of high frequencies at the transition from a liquid to a solid state is attributed by the appearance of additional force, preventing O-H bond bending. Deformation absorption band in IR-spectum of water has a frequency at 1645 cm-1 and very weak temperature dependence. It changes little in the transition to the individual H2O molecule at a frequency of 1595 cm-1. This frequency is found to be sufficiently stable, while all other frequencies are greatly affected by temperature changes, the dissolution of the salts and phase transitions. It is believed that the persistence of deformation oscillations is stipulated by processes of intermolecular interactions, e.g. by the change in bond angle as a result of interaction of H2O molecules with each other, as well as with cations and anions.
Thus the study of the characteristics of the IR spectrum of water allows to answer the question not only on the physical parameters of the molecule and the covalent bonds at isotopic substitution with deuterium, but also to make a certain conclusion on associative environment in water. The latter fact is important in the study of structural and functional properties of water associates and its isotopomers at the isotopic substitution with deuterium.
Conclusion
The experimental data obtained during the last years suggest that water is a complex dynamic associative system, consisting of tens and possibly hundreds individual H2O molecules binding by multiple intermolecular hydrogen bonds, being in a state of dynamic equilibrium. Up till now is scientifically proven the existence of associative water clusters with general formula (H2O)n, where n = 3–20. Although calculated structural models explain pretty well many anomalous properties of water and being in a good agreement with the experimental data on the diffraction of X-rays and neutrons, Raman, Compton scattering and EXAFS-spectroscopy, they are the most difficult to agree with the dynamic properties of water – flow, viscosity and short relaxation times, which are measured by picoseconds.
References:
1. Keutsch F., Saykally R. Water Clusters: Untangling the Mysteries of the Liquid, One Molecule at a Time // PNAS. 2011. V. 98. № 19. P. 105330–10540. Liu K., Cruzan J.D., Saykally R.J. Water clusters // Science Magazine. 1996. V. 271. № 5251. P. 929–933.
2. Pauling L. (ed.) The Nature of the Chemical Bond and the Structure of Molecules and Crystals. – New York: Cornell University Press, 1960.
3. Pasichnyk I. Everaers R. & Maggs A.C. Simulating van der Waals-interactions in water/hydrocarbon-based complex fluids // J. Phys. Chem. B. 2008. V. 112. № 6. P. 1761–1764.
4. Bernal J.D., Fowler R.H. A Theory of Water and Ionic Solutions, with Particular Reference to Hydrogen and Hydroxyl Ions // J. Chem. Phys. 1933. V. 1. P. 515–548.
5. Isaacs E.D., Shukla A., Platzman P.M. Compton scattering evidence for covalency of the hydrogen bond in ice // J. Phys. Chem. Solids. 2000. V. 61. P. 403–406.
6. Pimentel G.C., McClellan A.L. The hydrogen bond / L. Pouling, ed. – New York: Reinhold Publishing Co., 1960.
7. Arunan E., Desiraju G.R., Klein R.A. Definition of the hydrogen bond // Pure Appl. Chem. 2011. V. 83. №. 8. P. 1637–1641.
8. Antonov A., Galabova T. Reports from the 6th Nat. Conference of Biomedical Physics and Engineering. – Sofia, 1992.
9. Ignatov I., Mosin O.V. Structural mathematical models describing water clusters // Journal of Mathematical Theory and Modeling. V. 3. № 11. P. 72–87.
10. Bartha F., Kapuy O., Kozmutza C., Van Alsenoy C. Analysis of weakly bound structures: hydrogen bond and the electron density in a water dimmer // J. Mol. Struct. (Theochem). 2003. V. 666. P. 117–122.
11. Мosin О.V., Ignatov I. Structure of water // Himija. Izdatel'stvo 1 sentjabrja, Moscow 2012. V. 1. P. 12–32 [in Russian].
12. Ignatov I., Mosin O.V. The ice crystal riddles // Soznanije i physicheskaja realnost. 2013. V. 17. № 5. P. 21–31 [in Russian].
13. Michaelides A., Morgenstern K. Ice Nanoclusters at Hydrophobic Metal Surfaces // Nat. Mat. 2007. V. 6. P. 597–599.
14. Bai J., Wang J., Zeng C. Multiwalled Ice Helixes and Ice Nanotubes // Proc. Natl. Acad. Sci. 2006. V. 3. P. 104–117.
15. Timothy S., Zwier S. Chemistry: the Structure of Protonated Water Clusters // Science. 2004. V. 304. № 5674. P. 1119–1120.
16. Pople J.A. Molecular Association in Liquids: A Theory of the Structure of Water // Proceedings of the Royal Society. 1951. V. 205. P. 1081–1089.
17. Nemukhin A.B. The variety of clusters // Russian Chemical Journal. 1996. V. 40. № 2. P. 48–56.
18. Petkov V., Ren Y., Suchomel M. Molecular arrangement in water: random but not quite // J. Phys. Condens. Matter. 2012. V. 24. P. 155102.
19. Frenkel Y.I. Kinetic theory of liquids. – Leningrag: Nauka, 1975 [in Russian].
20. Henry S., Frank S., Wen-Yang Wen. Ion-solvent interaction. Structural Aspects of Ion-solvent Interaction in Aqueous Solutions: a Suggested Picture of Water Structure // Discuss. Faraday Soc. 1957. V. 24. P. 133–140.
21. Samoilov O.Ya. Studies of the structure of water // Journal of Structural Chemistry. 1963. V. 4. № 4. P. 459–461.
22. Domrachev G.A., Selivanovsky D.A. The Role of Sound and Liquid Water as Dynamically Unstable Polymer System in Abiogenous Production of Oxygen and the Origin of Life on the Earth, Preprint N 1'90. – Gorky: Inst. of Organometallic Chem. of the USSR Acad. Sci., 1990 [in Russian].
23. Antonov A. Research of the Nonequilibrium Processes in the Area in Allocated Systems. Diss. Thesis Doctor of Physical Sciences. – Sofia: Blagoevgrad, 2005.
24. Luck W., Schiöberg D., Ulrich S. Infared Iinvestigation of Water Structure in Desalination Membranes // J. Chem. Soc. Faraday Trans. 1980. V. 2. № 76. P. 136–147.
25. Saykally R. Unified Description of Temperature-Dependent Hydrogen Bond Rearrangements in Liquid Water // PNAS. 2005. V. 102. № 40. P. 14171–14174.
26. Sykes М. Simulations of RNA Base Pairs in a Nanodroplet Reveal Solvation-Dependent Stability // PNAS. 2007. V. 104. № 30. P. 12336–12340.
27. Loboda O., Goncharuk V. Theoretical study on icosahedral water clusters // Chemical Physics Letters. 2010. V. 484. № 4–6. P. 144–147.
28. Tokmachev A.M., Tchougreeff A.L., Dronskowski R. Hydrogen-Bond Networks in Water Clusters (H2O)20: An Exhaustive Quantum-Chemical // European Journal of Chemical Physics And Physical Chemistry. 2010. V. 11. № 2. P. 384–388.
29. Tsai C.J., Jordan K.D. Theoretical Study of the (H2O)6 Cluster // Chem. Phys. Letters. 1993. V. 213. P. 181–188.
30. Wang F., Jordan K.D. A Parallel Tempering Monte Carlo Investigation of (H2O)6- // J. Chem. Phys. 2003. V. 119. P. 11645–11653.
31. Maheshwary S., Patel N., Sathyamurthy N., Kulkarni A.D., Gadre S.R. Structure and Stability of Water Clusters (H2O)n, n = 8-20: An Ab Initio Investigation // J. Phys. Chem. 2001. V. 105. P. 10525–10537.
32. Choi T.N., Jordan K.D. Application of the SCC-DFTB Method to H+(H2O)6, H+(H2O)21, and H+(H2O)22 // J. Phys. Chem. B. 2010. V. 114. P. 6932–6936.
33. Zenin S.V. Structured water condition as a basis for controlling the behavior of living systems and safety. Diss. Doctor Biological Sciences. – Moscow: Institute of Medical Biological Problems, 1999 [in Russian].
34. Chaplin M. The Water Molecule, Liquid Water, Hydrogen Bonds and Water Networks / in: Water The Forgotten Biological Molecule, D.Le Bihan & H.Fukuyama (eds.). – Singapore: Pan Stanford Publishing Pte. Ltd, 2011.
35. Cui J., Liu H., Jordan K.D. Theoretical Characterization of the (H2O)21 Cluster: Application of an n-body Decomposition Procedure // J. Phys. Chem. 2006. V. 110. P. 18872–18878.
36. Мosin О.V., Ignatov I. Structure of water and physical reality // Soznanije i physicheskaja realnost, 10(1), 32–48 [in Russian].
37. Ignatov I., Mosin O.V. Mathematical models describing the nanostructure of water and nanoclusters // Nanoingenering, Izdatel'stvo Mashinostroenie, Moscow. 2013. №. 8. P. 32–46 [in Russian].
38. Ohno K., Okimura M., Akai N., Katsumoto Y. The effect of cooperative hydrogen bonding on the OH stretching-band shift for water clusters studied by matrix-isolation infrared spectroscopy and density functional theory // Phys. Chem. Chem. Phys. 2005. V. 7. P. 3005–3014.
39. Ignatov I., Mosin O.V. Structural models of water describing the cyclic clusters // Micro- and Nanosystem Technique. 2014. № 3. P. 47–56.
40. Wernet Ph., Nordlund D., Bergmann U. The structure of the first coordination shell in liquid water // Science. 2004. V. 304. P. 995–999.
41. Tokushima T., Harada Y., Takahashi O. High resolution X-ray emission spectroscopy of liquid water: The observation of two structural motifs // Chem. Phys. Lett. 2008. V. 460. P. 387–400.
42. Ignatov I., Mosin O.V. Methods for Measurements of Water Spectrum. Differential Non-equilibrium Energy Spectrum Method (DNES) // Journal of Health, Medicine and Nursing. 2014. Vol. 6. P. 50-72.
43. Zelsmann H.R. Temperature dependence of the optical constants for liquid H2O and D2O in the far IR region // J. Mol. Struct. 1995. V. 350. P. 95–114.
44. Yakhnevitch G.B. Infrared spectroscopy of water / G.B. Yakhnevitch. – Moscow: Nauka, 1973. 207 p. [in Russian].
45. Brubach J.B., Mermet A., Filabozzi A., Gerschel A., Roy P. Signatures of the hydrogen bonding in the infrared bands of water // J. Chem. Phys. 2005. Vol. 122. P. 184509.
46. Walrafen G.E. Raman and infrared spectral investigations of water structure / In Water a Comprehensive Treatise, F. Franks, Ed. – New York: Plenum Press. 1972. Vol. 1. P. 151–214.