The bifurcation rearrangement in cyclic water clusters: Breaking and making hydrogen bonds

M. G. Brown, F. N. Keutsch, and R. J. Saykallya

Department of Chemistry, University of California Berkeley, Berkeley, California 94720

Received 31 August 1998; accepted 30 September 1998

Бифуркатные перестановки в циклических водяных кластерах

Tunneling patterns observed in the vibration – rotation – tunnelling spectrum of H2O 5 measured
near 2.7 THz established the time scale for bifurcation rearrangements to be approximately 40 ns. 

This relatively local process is likely to be relevant in the dynamics of liquid water and ice. 

Rearrangements of the hydrogen-bond network in water
clusters are manifested as intricate quantum mechanical tun
neling splittings in their vibration – rotation – tunneling VRT
spectra. Detailed study of these tunneling dynamics in water
clusters can provide new insight into the corresponding ther
mally activated rearrangement processes that occur in con
densed phases. The term bifurcation’’ describes a
hydrogen-bond network rearrangement HBNR observed in
most of the water clusters studied so far by high-resolution
VRT spectroscopy viz. the water dimer, trimer, and probably
hexamer although explicitly not observed in the water
tetramer.1 – 6 In this process, the hydrogen bonds on a particu
lar water monomer are broken and then reformed by quan
tum tunneling through a transition state lying 2 kcal/mol
above the potential minimum and having a bifurcated
hydrogen-bond arrangement7 Fig. 1 . Here, we present the
results of a new study of the water pentamer in which the
corresponding bifurcation rearrangement has been character
ized for the rst time. The results have interesting implica
tions for the dynamics of solid and liquid water. 

While the bifurcation rearrangement has been thor
oughly characterized in the H2O, D2O, and mixed isotope
forms of the water dimer8 – 10 and water trimer,4,11 it was not
observed in previous studies of the water pentamer. Both
calculations13 and experiments6 have recently shown that the
properties of the hydrogen-bond networks in small water
clusters converge rapidly to condensed phase values, such
that the water pentamer already exhibits H-bond lengths,
monomer dipole moments, and bond energies comparable to
average values found in liquid water and ice. The potential
energy barrier for the bifurcation rearrangement in the pen
tamer can be expected to correspond approximately to that of
double hydrogen-bonded monomers present in the con
densed phases and to be a lower limit for those with more
than two hydrogen bonds. The effective mass and path
length should remain approximately constant with cluster
size, i.e., it is a relatively local process. Characterization of
the bifurcation rearrangement in the water pentamer will,
therefore, help to constrain the time scale for the correspond
ing unactivated T 0 K process in the condensed phases of
water. 

Walsh and Wales WW 7 predicted that bifurcation tun
neling would be too small to resolve in D2O 5, but that it
should indeed be observable in H2O 5. Their group theoret
ical analysis predicted a multiplet pattern of six lines with
intensity ratios of 1:3:18:54:81:51 for VRT transitions hav
ing angular momentum projection quantum number K equal
to a multiple of 5 and 0:3:18:54:81:48 for all other VRT
transitions. These intensity ratios were computed from
nuclear spin weights of the irreducible representations of the
permutation – inversion group G 320 . The magnitude of the
tunneling splittings was predicted to be 0.2 GHz from diffu
sion quantum Monte Carlo calculations by Gregory and
Clary,12 using the ASP – NB water potential. 

We recently observed a VRT spectrum of H2O 5 near
90 cm 1 2.670 303 7 6 THz that revealed the spectral
splitting pattern predicted by WW Fig. 2 . A total of 200
individual transitions were precisely measured 3.13 MHz
and t to a standard symmetric top energy-level expression
Eq. 1 including rst-order Coriolis perturbations. Sepa
rate centrifugal distortion constants were used for the
components of the Coriolis perturbations. In recent theoreti
cal studies of the water trimer by van der Avoird14 it was
shown that these rst-order’’ Coriolis effects actually result
from second-order coupling between hydrogen torsion and
the overall rotation of the water trimer, and a similar mecha
nism may be operative in the case of the water pentamer. 

Each VRT transition was split by bifurcation tunneling into
six lines separated by 4.8 MHz and having the predicted
relative intensities Fig. 2 . However, the small nuclear spin
weights of the weakest two of these tunneling components
precluded their observation. 

The water pentamer is predicted by ab initio theory13 to
have a puckered pentagonal global equilibrium structure
similar to that of cyclopentane. The results of the spectral
analysis show that this asymmetric equilibrium structure
which, as for the water trimer, is chiral vibrationally aver
ages to that of a symmetric top. This vibrational averaging of
the oxygen framework was previously observed in the D2O
form of the water pentamer,6 and thus was expected to occur
in the H2O form as well. It seems likely that the many low
frequency vibrational modes predicted by ab initio theory13
ten normal modes are predicted below 200 cm 1) provide a
mechanism for averaging the oxygen framework to a quasi
planar structure, while free-hydrogen ipping’’ dynamics
similar to those characterized in the water trimer4 will aver
age the hydrogen positions. The resulting average structure
has C 5 h symmetry. Explicit vibrational assignment of the
observed transition is dif cult at this time since there are so
many low-frequency modes. The Coriolis perturbations ob
served, through comparison with perturbations observed in
the water trimer, are consistent with assignment to a transi
tion between doubly degenerate torsional energy levels.

The bifurcation tunneling motion described for the water
pentamer in Fig. 1 has now been observed in the water
dimer, trimer, pentamer, and hexamer, and speci cally, is not
observed in the water tetramer.1,3 – 6 In the water dimer the
bifurcation tunneling motion has typically been referred to as
donor tunneling’’ as it exchanges the role of the bound and
free protons on the donor water molecule.9 The motion can
be described as a geared rotation of both the donor and ac
ceptor water molecules about axes perpendicular to the plane
of symmetry of the cluster. The barrier to this motion has
been predicted by ab initio theory15 to be 658 cm 1 without
zero-point correction. The tunneling motion is manifested in
spectral shifts of approximately 1 GHz in the relative ener
gies of the various symmetry components of each vibrational
band. These shifts are dependent on the approximate quan
tum number K a of the transition. Shifts, rather than split
tings, occur because the other tunneling motions of the dimer
acceptor switching and donor – acceptor interchange allow
the same rearrangements to occur through different mecha
nisms with lower barriers, effecting the maximum degree of
splitting allowed by symmetry. Bifurcation rearrangement in
the water trimer has been studied in detail by van der Avoird
et al.16,17 A comparison of their theory and our experimental
results revealed that the tunneling motion for this process

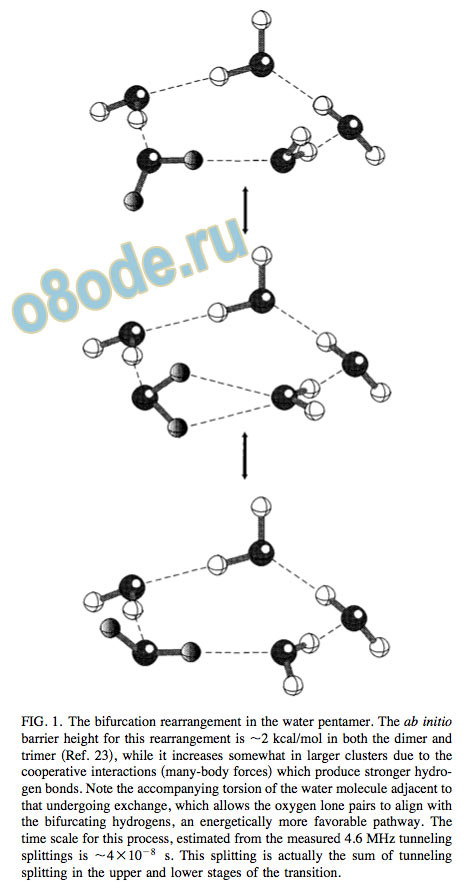
FIG. 1. The bifurcation rearrangement in the water pentamer.

The ab initio barrier height for this rearrangement is 2 kcal/mol in both the dimer and
trimer Ref. 23 , while it increases somewhat in larger clusters due to the
cooperative interactions many-body forces which produce stronger hydro
gen bonds. Note the accompanying torsion of the water molecule adjacent to
that undergoing exchange, which allows the oxygen lone pairs to align with
the bifurcating hydrogens, an energetically more favorable pathway. The
time scale for this process, estimated from the measured 4.6 MHz tunneling
splittings is 4 10 8 s. This splitting is actually the sum of tunneling
splitting in the upper and lower stages of the transition.

FIG. 2. VRT spectrum of ( H2O 5 measurement near 89 cm 1. A stick spec
trum representation of the Q branch. The repelling Q branches clearly show
the in uence of linear Coriolis mixing of degenerate torsional states, while
the inset shows the bifurcation tunneling splittings present in each line in the
spectrum. The rotational constants B and B extracted from this spectrum
are 1989.45 7 and 1992.46 7 MHz, respectively, and the vibrational band
origin is 2.6703037 6 THz. This spectrum was taken with the Berkeley
terahertz spectrometer, which can be brie y described as follows. A line
tunable CO2 laser pumps a terahertz laser and the resulting xed frequency
light is mixed with tunable microwave radiation on a Schottky barrier diode
to produce tunable sidebands of frequency laser microwave . These
tunable sidebands are multipassed in the throat of a pulsed planar supersonic
expansion of argon and H2O and detected with a stressed germanium/
gallium photoconductive detector. 

requires a neighboring water molecule to ip’’ its free pro
ton from one side of the cluster to the other via torsion about
the H bond. This motion can be viewed as an extension of
the geared’’ motion observed in the water dimer and is
similar to the mechanism shown for the pentamer in Fig. 1. 

The barrier for this process has been calculated by ab initio
methods18 to be 823 cm 1 and results in a quartet splitting
expressed as the difference between upper and lower state
tunneling splittings in our spectra of 289 MHz. Terahertz
spectra of the H2O and the D2O forms of the water tetramer
have revealed no tunneling splittings attributed to bifurcation
tunneling.3 The cause of this is probably the inability of the
highly symmetric tetramer structure to undergo a geared bi
furcation pathway. Rather, such tunneling must arise from a
pure C2 exchange pathway, a pathway that exhibits an unob
servably high barrier to exchange. The global minimum af
ter zero-point energy corrections of the water hexamer is a
three-dimensional cage structure with constituent water mol
ecules in several distinct donor – acceptor roles.

Four of the molecules are involved in three hydrogen bonds, while two
are doubly bonded. The two doubly bonded water molecules
undergo a hydrogen-bond rearrangement by an as yet un
known pathway. Recent work by Wales in ambiguous on this
topic, bifurcation and nonbifurcation pathways being ap
proximately equally weighted.19 No exchange motions have
yet been observed for the triply bonded water molecules.
An interesting comparison can be made between bifur
cation rearrangements in small water clusters and similar
hydrogen-bond rearrangement processes occurring in liquid
water and ice. For example, it is known that the proton
disordered phases of ice have large dielectric permittivities20
97.5 for ice Ih to 193 for ice VI , larger even than for
liquid water ( 8 8 ) . These values are 30 – 50 times larger
than the dielectric constants for the proton-ordered phases
ice II and ice IX . This suggests that some highly effective
relaxation mechanism is available to proton-disordered ice,
allowing it to reorient ef ciently in an electric eld. It has
been proposed that defects in the ice lattice are the main
contribution to this reorganization.21 In such a model,
phonons in the ice lattice cause hydrogen bonds to break or
weaken. With a suf cient number of hydrogen bonds broken,
the water molecules in the ice lattice can reorient by tunnel
ing, perhaps through a bifurcated transition state. These ideas
are supported by temperature-dependent quantum
mechanical calculations of the dielectric relaxation time of
ice Ih by Bruni et al.22 They found that quantum tunneling
was the dominant reorganizational mechanism contributing
to the dielectric relaxation time at temperatures below 230 K. 

Signi cantly, they found that quantum corrections to classi
cal rotations were required to explain the experimental data
at all temperatures. The calculated relaxation times ranged
from 102 to 104 s over the temperature range 260 – 210 K. 

This time frame is consistent with the bifurcation tunneling
time in the water pentamer 40 ns , estimated from our
tunneling splitting of 4.8 MHz. Although the intermediate
states in the reorganization of ice are still unknown, it is
possible that bifurcation rearrangement is an essential feature
of this process. This certainly deserves further investigation.
Other examples wherein bifurcation tunneling may af
fect the bulk properties of liquid water and ice are known,
viz. depolarized Rayleigh Raman scattering23,24 and quasi
elastic neutron scattering experiments.25 In these experi
ments on liquid water, classical reorganization is more domi
nant than in the solid. Reorganization times are ps,
comparable to hindered rotation in liquid water. Even in
these systems, however, quantum reorganization terms often
referred to as jump diffusion’’ terms are necessary to t
experimental data to experimental precision. This tunneling
reorganization process may well involve bifurcation tunnel
ing. In any case, the exact role of the bifurcation rearrange
ment in the dynamics of water and ice remains an interesting
problem. We hope that the results reported here facilitate
further efforts. 

This work was supported by the Experimental Physical Chemistry program of the National Science Foundation. 

1
K. L. Busarow, R. C. Cohen, G. A. Blake, K. B. Laughlin, and R. J.
Saykally, J. Chem. Phys. 90, 3937 1989 .
2
R. J. Saykally and G. A. Blake, Science 259, 1570 1993 .
3
J. D. Cruzan, L. B. Braly, K. Liu, M. G. Brown, and R. J. Saykally,
Science 271, 59 1996 .
4
K. Liu, J. G. Loeser, M. J. Elrod, B. C. Host, and R. J. Saykally, J. Am.
Chem. Soc. 116, 3507 1994 .
5
K. Liu, M. G. Brown, C. Carter, R. J. Saykally, J. K. Gregory, and D. C.
Clary, Nature London 381, 501 1996 .
6
K. Liu, M. G. Brown, J. D. Cruzan, and R. J. Saykally, Science 271, 62
1996 .
7
D. J. Wales and T. R. Walsh, J. Chem. Phys. 105, 6957 1996 .
8
T. R. Dyke, J. Chem. Phys. 66, 492 1977 .
9
G. T. Fraser, F. J. Lovas, R. D. Seunram, E. N. Karyakin, A. Grushow, W.
A. Burns, and K. R. Leopold, J. Mol. Spectrosc. 181, 229 1997 .
10
E. Zwart, J. J. ter Meulen, W. L. Meerts, and L. H. Coudert, J. Mol.
Spectrosc. 147, 27 1991 .
11
M. R. Viant, J. D. Cruzan, D. D. Lucas, M. G. Brown, and R. J. Saykally,
J. Phys. Chem. A 101, 9032 1997 .
12
J. K. Gregory and D. C. Clary, J. Chem. Phys. 105, 6626 1996 .
13
S. S. Xantheas and T. H. Dunning, Jr., J. Chem. Phys. 99, 8774 1993 .
14
M. R. Viant, M. G. Brown, J. D. Cruzan, R. J. Saykally, A. van der
Avoird, and Michel Geleijns submitted .
15
B. J. Smith et al., J. Chem. Phys. 92, 1240 1990 .
16
A. van der Avoird, E. H. T. Olthof, and P. E. S. Wormer, J. Chem. Phys.
105, 8034 1996 .
17
A. van der Avoird, E. H. T. Olthof, and P. E. S. Wormer, J. Chem. Phys.
105, 8051 1996 .
18
D. J. Wales, J. Am. Chem. Soc. 115, 11180 1993 .
19
D. J. Wales, in Advances in Molecular Vibrations and Collision Dynam
ics, edited by Z. Bacic and J. Bowman JAI, Greenwich, CT, 1997 .
20
G. W. S. Robinson, S. Zhu, S. Singh, and M. W. Evans, Water in Biology,
Chemistry and Physics World Scienti c, Singapore, 1996 .
21
N. Bjerrum, Science 115, 385 1952 .
22
F. Bruni, G. Consolini, and G. Careri, J. Chem. Phys. 99, 538 1993 .
23
O. Conde and J. Teixeira, Mol. Phys. 53, 951 1984 .
24
O. Conde and J. Teixeira, J. Phys. France 44, 525 1983 .
25
F. Cavatorta, A. Deriu, D. Di Cola, and H. D. Middendorf, J. Phys. Con
dens. Matter 6, 113 1994 .
9647
J. Chem. Phys., Vol. 109, No. 22, 8 December 1998 Communications