Structure and Stability of Water Clusters
Structure and Stability of Water Clusters (H2O)n, n= 8-20: An Ab Initio Investigation
Shruti Maheshwary, Nitin Patel, and Narayanasami Sathyamurthy Department of Chemistry, Indian Institute of Technology, Kanpur, 208 016 India Anant D. Kulkarni and Shridhar R. Gadre Department of Chemistry, UniVersity of Pune, Pune, 411 007 India ReceiVed: August 15, 2001
Extensive ab initio calculations have been performed using the 6-31G(d,p) and 6-311++G(2d,2p) basis sets for several possible structures of water clusters (H2O)n, n ) 8-20. It is found that the most stable geometries arise from a fusion of tetrameric or pentameric rings. As a result, (H2O)n, n ) 8, 12, 16, and 20, are found to be cuboids, while (H2O)10 and (H2O)15 are fused pentameric structures. For the other water clusters (n ) 9, 11, 13, 14, and 17-19) under investigation, the most stable geometries can be thought of as arising from either the cuboid or the fused pentamers or a combination thereof. The stability of some of the clusters, namely, n ) 8-16, has also been studied using density functional theory. An attempt has been made to estimate the basis set superposition error and zero-point energy correction for such clusters at the HartreeFock (HF) level using the 6-311++G(2d,2p) basis set. To ensure that a minimum on the potential-energy surface has been located, frequency calculations have been carried out at the HF level using the 6-31G(d,p) and 6-311++G(2d,2p) basis sets for some of the clusters. Molecular electrostatic potential topography mapping has been employed for understanding the reactivity as well as the binding patterns of some of the structurally interesting clusters.
1. Introduction
“Water clusters”, groups of water molecules held together by hydrogen bonds, have been the subject1 of a number of intense experimental and theoretical investigations because of their importance in understanding cloud and ice formation, solution chemistry, and a large number of biochemical processes. The exploration of the structural and binding properties of water clusters is the first step to understanding the properties of bulk water, the nectar of life. The difficulty in obtaining a rigorous molecular scale description of the structure of liquid and solid water largely is due to the extended hydrogen-bonding network therein and its soft modes. There are numerous local minima on the potential-energy hypersurface of water clusters, the number of which grows rapidly with increasing cluster size, thus making the search for global minima a computationally demanding job.
Substantial progress has been made in recent years in the study of the structure of water clusters. From a theoretical point of view, many different models of water clusters have been studied with the aim of understanding the characteristics of hydrogen bonds. A number of ab initio calculations have also been carried out to investigate the strength of the hydrogen bonds and their cooperativity. Some of the recent reviews on the subject can be found elsewhere.2-4
The water dimer, the smallest water cluster which constitutes the fundamental step in the study of water clusters, has been studied in great detail experimentally5-11 as well as theoretically.12-25 It has been established that the most stable structure of a water dimer is of the Cs symmetry and that it has a single hydrogen bond with a strength of 5.5 ( 0.7 kcal/ mol.5-11
Vibrational spectroscopic studies26 as well as some of the early ab initio studies27 suggested an open-chain conformer with nearly linear hydrogen bonds as the most stable structure of a water trimer. Some of the other experimental28-30 and theoretical31-39 studies show a cyclic structure with C1 symmetry, with two external hydrogen atoms on one side of the O-O-O plane and a third one on the other side of the plane, to be the most stable. In such a structure, each monomer behaves as a donor as well as an acceptor. Perhaps the most interesting feature of the trimer structure deduced by vibration-rotationtunneling (VRT) spectroscopy29 is its chiral nature, with a low barrier to the quantum tunneling motion interconverting the leftand right-handed stereoisomers.
Ab initio calculations12,16,19,21,23,24,38,40,41 have established a homodromic cyclic structure with S4 symmetry to correspond to the global minimum for the tetramer. In this case, the “free” hydrogen atoms alternate in their arrangement above and below the plane of the O-O-O-O ring. Infrared (IR) spectra of benzene-(H2O)411 and VRT spectra of (D2O)442 and (H2O)443 showed an equilibrium structure with S4 symmetry having the concerted flipping motions of the free H atoms for the tetramer. Pentagonal rings of water molecules appear to be ubiquitous in nature, for example, in clathrate hydrates and in the solvation of hydrophobic groups of small molecules as well as in proteins and in DNA molecules. The most stable structure for the pentamer follows the same cyclic ring pattern as that observed for the trimer except that it is puckered.1,11,44-46 It is also chiral. Ab initio calculations12,15,20,23,38,40,47,48 also predicted such a ring structure. Burke et al.,48 for example, examined various Author for correspondence: Honorary Professor Jawaharlal Nehru Centre for Advanced Scientific Research, Jakkur, Bangalore 560 064, India. E-mail: nsath@iitk.ac.in.
E-mail: gadre@chem.unipune.ernet.in. 10525 J. Phys. Chem. A 2001, 105, 10525-10537 10.1021/jp013141b CCC: $20.00 © 2001 American Chemical Society
Published on Web 10/30/2001
structures of pentamers at the Hartree-Fock (HF) level and found that the ring was more stable than the bipyramidal forms by at least 1 kcal/mol. Wales49 pointed out the existence of different ring structures that can be interconverted through lowenergy barrier pathways consisting of the flipping of hydrogen atoms and bifurcation mechanisms.
The structure of (H2O)6 represents a transition from cyclic to three-dimensional geometries, and it has been studied extensively by theory and experiments. Although some of the ab initio calculations15,16,19,50-52 suggested the cyclic and the prismatic structures to be the most stable, it has recently become clear40,53-58 that a large number of alternative three-dimensional structures, such as chair, boat, and cage, are likely to be of comparable energies. Perhaps the first experimental evidence for the cage structure came from the work of Pribble and Zwier11 from their study of the C6H6-(H2O)6 adduct. Liu et al.1,59,60 verified through their FIR-VRT spectroscopy experiments that the isolated water hexamer does have a cage structure. Zeropoint vibrational energy (ZPE) seems to play an important role in deciding the preferred geometry of the hexamer. A detailed study on water hexamer cages at the semiempirical (PM3) level has been carried out recently by Coe et al.58b Diffusion quantum Monte Carlo calculations23,61 predict the cage structure to be the most stable, and the computed properties, such as rotational constants, dipole moment, and so forth, are in agreement with the experimental results.
Size-specific IR spectra of benzene-(H2O)7 clusters11 suggest a compact noncyclic structure for (H2O)7. IR-UV and UVUV double resonance spectra of jet-cooled phenol-(H2O)7 clusters supported a cuboid structure for the heptamer, with one corner being occupied by the phenolic oxygen atom.62 The vibrational O-H spectra of pure (H2O)763 indicate the existence of two isomers derived from the S4 octamer cube by the removal of either a double-donor or a double-acceptor water molecule. With the increase in the size of the cluster, the number of possible structures increases rapidly, and it becomes difficult to probe all of the conformers. Therefore, theoretical studies until this date40,64-66 have tended to focus on a few of them: seven-membered cyclic structures as well as cages made up of different cyclic n-mers fused together. The consensus seems to be that there are several cage structures lying close to each other, with the cuboidal geometry (with a corner missing) being the lowest in energy.
Extensive ab initio calculations16,40,53,57,67,68 suggest that, at low temperatures, (H2O)8 would stabilize into a cube with D2d or S4 symmetry and that, at higher temperatures, entropy considerations could favor the other geometries. Experiments involving pure water clusters69a as well as hydrated molecules, such as C6H6-(H2O)870 and phenol-(H2O)8,62 are supportive of the cubic structure for the octamer.
Jensen et al.71 considered 44 possible structures for the nonamer in their extensive HF calculations using the 6-311G(d) and 6-311G(d,p) basis sets and concluded that the most stable structure consisted of a four-membered ring stacked over a fivemembered ring that could be thought of as an extended cube. The only available experimental result for (H2O)969a seems to be in qualitative agreement with the predicted structure. The O-H stretch spectra of (H2O)1069a seem to support a butterfly structure and not a fused cage.
Recently, Lee et al.69b have carried out ab initio computations at the DFT/B3LYP/6-311G(d,p) and MP2/DZP levels with a view to determine the structure, energies, vibrational spectra, and electronic properties of the clusters for (H2O)n, n ) 1-10. Their study involves a detailed comparison of the theoretical results at different levels of theory with the experimental findings, although a few structures for n g 7 are missing. To the best of our knowledge, there are no experimental results available for (H2O)n, n > 10. There have been some theoretical studies using semiempirical potentials, and there have been very few ab initio studies. For instance, Tsai and Jordan72 found that the TIP4P potential73 for water clusters favored a cuboid geometry over the hollow cage for n ) 12, 16, and 20. Their MP2 calculations confirmed that the cuboid geometry was the most stable for n ) 12. Additional calculations by Sremaniak et al.74 supported the stacked cubic structure of the D2dD2d symmetry over the stacked cyclic hexamers of the S6 symmetry. MNDO-PM3 calculations75 also suggested the cuboid geometries to be the most stable for (H2O)12 and (H2O)16. Kirschner and Shields76 predicted cuboids and fused pentameric structures to be the most stable for (H2O)20. Interestingly, on the basis of his semiempirical calculations at the INDO level, Khan77 concluded that stacked cubes are unlikely to be formed and that cage structures are more likely as the size of the cluster increases. He has proposed78 several different cage structures for (H2O)n, n ) 24-35. Some of them are fused and have free water molecules inside the cage.
We have carried out a systematic study of water clusters, from dimer to 20-mer using restricted HF and density functional theory (DFT) calculations. Although clusters of the sizes 2-8 have been the subject of a number of earlier ab initio investigations, we have repeated some of them so that a comparison could be made with the larger clusters in a consistent manner.
2. Methodology
We have used the “supermolecule” approach to optimize the geometries and to compute the stabilization energies of the water clusters at the HF level of theory using the GAUSSIAN94 suit of programs.79 A computationally manageable, large basis set, 6-31G(d,p), has been employed in the present study. To study the effect of the size of the basis set on the energetics, the structures obtained initially at the HF/6-31G(d,p) level were further studied using a larger basis set, 6-311++G(2d,2p), that employs 47 contractions per water molecule. Several workers have used the DFT approach to study hydrogen-bonded16,20,55 clusters. The success of some of these investigations could be attributed to the fact that the DFT approach includes exchange correlation effects. On the basis of the success of these studies, B3LYP parametrization with the 6-31G(d,p) basis set has been used in the present study for (H2O)n, n e 16.
In view of the large number of possible geometries for the larger clusters, there would be several minima on a shallow potential-energy surface, and it becomes extremely difficult to locate the true energy minimum for each cluster. Nevertheless, we could ascertain that the minimum-energy structures reported in this study indeed corresponded to (at least local) minima by calculating the vibrational frequencies at the HF/6-31G(d,p) and HF/6-311++G(2d,2p) levels for some of the clusters and ensuring that they were real.
To understand the reactivity patterns of the water clusters, molecular electrostatic potential (MESP) topography mapping has been done for the HF-optimized geometries for some of the clusters. MESP, V(r), generated by the nuclear charges and molecular electron distribution is defined as where the first term stands for the contribution due to the nuclei with charges ZA located at RA and the second term is due to the continuous distribution of electronic charge density, F(r). The critical points (CPs) are the points at which all three of first partial derivatives of the function under investigation vanish [i.e., V(r) ) 0].
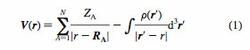
CPs provide valuable information about the structure and the environment of the molecule. A more detailed discussion of the MESP and the CPs can be found elsewhere.80 The molecular property calculation program UNIPROP81 was employed for the topographical analysis. The visualization of MESP was effected by employing a recently developed userfriendly visualization package, UNIVIS-2000.82
3. Results and Discussion
For the smaller water clusters, we initiate the HF calculation using one of the reported stable geometries as a starting point. This involves typically rO-H ) 0.959 Å and HOH ) 105.0° for the monomer.83a Geometries and stabilization energies obtained from geometry optimization calculations at the HF/631G(d,p) level of theory for (H2O)n, n ) 2-5, are reported in Figure 1 and Table 1, and they are consistent with the results reported in the literature.
Optimized geometries and stabilization energies (SE) for the larger clusters, obtained from HF/6-31G(d,p) calculations are reported in Tables 1-4 and in Figures 1-15. To check the influence of the level and the size of the basis set on the results, calculations have been carried out at the HF, DFT/B3LYP, and MP2 levels using the 6-311++G(2d,2p) basis set. Results for n ) 2-7 are presented in Table 1, and those for n ) 8-10 are included in Table 2.
For n ) 11-20, we have carried out single-point HF calculations using the 6-311++G(2d,2p) basis set at HF/6-31G(d,p) optimized geometries, and the results are reported in Tables 2-4.
For n ) 6, the cage structure (see Figure 1) has been reported to be the most stable from both experimental and theoretical points of view.23,53,56 Our calculations, however, show that the prism structure with nine O-H bonds is more stable than the cage structure with eight O-H bonds, if we do not take into account the ZPE correction (compare to Table 1). If we include the ZPE correction, the cage structure is found to be more stable than the prism by 0.19 kcal/mol at the HF/6-311++G(2d,2p) level. Details of the results with ZPE and BSSE corrections are given in Table 5 and discussed later in the text. Application of both the corrections at the same time is known to overcorrect the results.83b,c
For n ) 7, a cubelike structure (Figure 2, structure 7A) with a corner missing, is found to be the most stable. This structure has 10 hydrogen bonds and has an SE of -60.53 kcal/mol at the HF/6-31G(d,p) level, with a dipole moment (µ) of 1.35 D. The structure 7B that is closest to 7A in energy lies higher by 1.5 kcal/mol, and it has only nine hydrogen bonds. It is nearly cubic but has a higher dipole moment of 4.33 D, indicating asymmetry. The structure 7C is like a basket with a square base. Although it has nine hydrogen bonds, it is 2.7 kcal/mol higher in energy than 7B and has a smaller dipole moment. Structures 7D and 7E are bicyclic, with comparable SE and the same number of hydrogen bonds.
The O-H bond that is not inVolVed in a hydrogen bond is referred to as “free” hydrogen (Hf), and it has a bond distance of 0.943 Å for the structure 7A. The one that is inVolVed in a hydrogen bond is referred to as “bridged” (Hb), and it has different rO-Hb values in the different hydrogen bonds in the heptamer, but they are all in the vicinity of 0.955 Å. Characteristically, they are larger than the rO-Hf values, as has been known for all of the hydrogen bonds in the literature. The Figure 1. Schematic representation of the most stable geometry for (H2O)n, n ) 2-6, along with the stabilization energy (SE) values in kcal/mol and the number of hydrogen bonds (nH) as obtained from HF calculations using the 6-31G(d,p) basis set. The values in parentheses correspond to SE values obtained from DFT calculations using B3LYP parametrization.
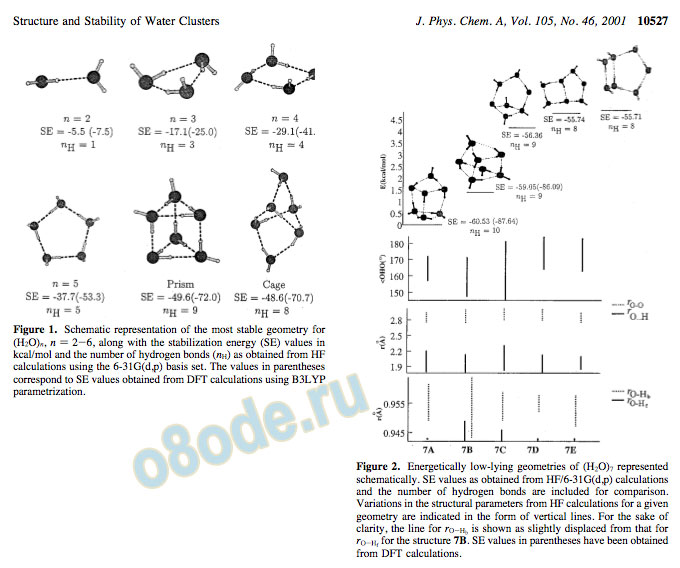
Figure 2. Energetically low-lying geometries of (H2O)7 represented schematically. SE values as obtained from HF/6-31G(d,p) calculations and the number of hydrogen bonds are included for comparison. Variations in the structural parameters from HF calculations for a given geometry are indicated in the form of vertical lines. For the sake of clarity, the line for rO-Hb is shown as slightly displaced from that for rO-Hf for the structure 7B. SE values in parentheses have been obtained from DFT calculations.
Structure and Stability of Water Clusters J. Phys. Chem. A, Vol. 105, No. 46, 2001 10527 distance rO-H between the covalently bonded H and the nearest neighbor O atom involved in the hydrogen bond has values in the vicinity of 2.0 Å, falling in the expected84 range of 1.72.45 Å. Because most of the hydrogen bonds in 7A are not exactly linear (OHO 160-170°), the distance rO‚‚‚O between the neighboring oxygen atoms involved in a hydrogen bond is around 2.8 Å, slightly less than the sum of rO-Hb and rO-H.
It is evident from the different plots in Figure 2 that the values of rO-Hf, rO-Hb, rO‚‚‚O, rO-H, and OHO for the different possible low-energy structures of (H2O)7 fall within the ranges expected for the hydrogen-bonded water clusters, with HOH ranging between 103° and 107°. Our finding that the cubelike structure 7A is the most stable for the heptamer is in agreement with the DFT/HF/MP2 results reported recently.20,64,66,69 A similar trend in the energetics was observed for the three low-energy conformers 7A-C at the HF/6-311++G(2d,2p) level, as illustrated in Table 1.
The most stable geometry of (H2O)8 is cubic 8A, with D2d symmetry and thus µ ) 0.0, having 12 hydrogen bonds and an SE of -76.01 kcal/mol. An alternative nonpolar cubic structure (8B) lying close in energy (-75.89 kcal/mol) has also been observed. At the HF/6-311++G(2d,2p) level of optimization, structure 8B is found to be isoenergetic to structure 8A, and structure 8C is higher in energy by 2.25 kcal/mol. Yet, another set of cuboids (8D-F) of lower symmetry (Ci, C1, and C2) and slightly higher energy also exists as depicted in Figure 3 and listed in Table 2. The norbornane structure 8G has only 10 hydrogen bonds and is distinctively higher in energy. The cubic geometry (D2d) of the hydrogen-bonded (H2O)8 described previously is in conformity with the structures reported independently by Gruenloh et al.,70 Janzen et al.,62 and Buck et al.69a from their experiments.
As anticipated from the experimental studies of Buck et al.,69a the nonamer has one water molecule hydrogen bonded (“twocoordinated”) to the cubic octamer, as shown in Figure 4 as structure 9A. It has 13 hydrogen bonds (the cube has 12), an SE of -85.05 kcal/mol, and µ ) 1.69 D. It must be pointed out that one of the edge hydrogen bonds in the cube is broken
TABLE 1: Number of Hydrogen Bonds (nH) and Stabilization Energies (SE, kcal/mol) for Water Clusters, (H2O)n, n ) 1-7 SE 6-31G(d,p) 6-311++G(2d,2p)
TABLE 2: nH and SE (kcal/mol) of (H2O)n, n ) 8-16, at Various Levels of Theory Using 6-31G(d,p) and 6-311++G(2d,2p)
6-31G(d,p) 6-311++G(2d,2p)
molecule structure code nH HF DFT/B3LYP HF DFT/B3LYP MP2a
MP2/6-311++G(2d,2p) single-point energy calculation at the MP2/6-31G(d,p) optimized geometry. b HF/6-311++G(2d,2p) single-point energy
calculation at the HF/6-31G(d,p) optimized geometry.
10528 J. Phys. Chem. A, Vol. 105, No. 46, 2001 Maheshwary et al.
and a hydrogen bond is formed with the ninth water molecule. The structure 9C, having the octameric cube nearly intact and the ninth water molecule forming hydrogen bonds with the corners of the cube, is distinctively higher in energy (SE ) -79.16 kcal/mol). Interestingly, a more distorted structure (9B) that has a fused tetramer-pentamer structure is lower in energy (SE ) -80.63 kcal/mol) than 9C. As a matter of fact, geometry optimization starting from a water molecule encapsulated inside the cube of an octamer results in 9B. It must be pointed out that structure 9C has 14 hydrogen bonds, while 9A and 9B have only 13 hydrogen bonds. Yet, 9B and 9C are energetically less stable than 9A. Earlier studies have shown that the structures involving fused trimers are less stable than those involving tetramers and pentamers. Structures 9D and 9E are trigonal prismlike and are higher in energy. The details of the energies at both the HF and DFT levels, along with the dipole moments, are given in Table 2.
Buck et al.69a have proposed the possibility of two water molecules two-coordinated to the “edge” water molecule in a cube, resulting in a fused pentameric structure for (H2O)10. However, their experiments seemed to suggest a butterfly minimum. Our calculations at the HF/6-31G(d,p) level showed the fused pentameric structure 10A to be energetically the most stable, with 15 hydrogen bonds and SE ) -96.75 kcal/mol, as illustrated in Figure 5. The butterfly minimum (10C) is higher in energy than 10A by 2.87 kcal/mol. There is an extended cuboid structure (10B) that lies energetically between 10A and 10C. A highly symmetrical structure (µ ) 0.0), with 16 hydrogen bonds (10D), was considered for (H2O)10 by considering the two water molecules that are two-coordinated diagonally on opposite faces of a cube, but it turned out to be much less stable than the other three geometries discussed previously. There are no experimental results available, to the best of our knowledge, for (H2O)n, n g 11. However, considering the good qualitative agreement between experiment and theory for (H2O)n, n e 10, it was felt that it would be worth extending the study to (H2O)n, n > 10. An account of our results obtained using HF calculations with the 6-31G(d,p) and 6-311++G(2d,2p) basis sets for 11 e n e 20 follows.
The most stable geometry for the 11-mer is a fused pentamer, with the 11th water molecule hydrogen bonded to one of the corners as illustrated in Figure 6. If the geometry of the nonamer could be thought of as an extension of a cube, then the geometry of the 10-mer could be considered as another extension of the cube, resulting in a fused pentameric structure. In other words, the fused pentamer could be considered as an extension of the cuboid. If the 12-mer is a cuboid (12A), then the 11-mer could have a stable geometry that corresponds to a cuboid with a
TABLE 3: nH and SE (kcal/mol) at Different Levels of Theory for (H2O)n, n ) 13-16
SE
molecule structure code nH HF/6-31G(d,p) HF/6-311++G(2d,2p)a DFT/B3LYP/6-31G(d,p)
HF/6-311++G(2d,2p) single-point energy calculation at the HF/6-31G(d,p) optimized geometry.
TABLE 4: nH and SE (kcal/mol) for (H2O)n, n ) 17-20
SE
HF
molecule structure code nH 6-31G(d,p) 6-311++G(2d,2p)a
HF/6-311++G(2d,2p) single-point energy calculation at the RHF/ 6-31G(d,p) optimized geometry.
TABLE 5: Effect of BSSE and ZPE Corrections on SE (kcal/mol) at the HF/6-311++G(2d,2p) Level for (H2O)n, n )
Structure and Stability of Water Clusters J. Phys. Chem. A, Vol. 105, No. 46, 2001 10529
missing corner. Such a geometry (11B) is indeed stable but slightly higher in energy than the fused pentameric structure (11A), as shown in Figure 6.
For the 12-mer of water clusters, we have considered different geometries that are cuboid, fused pentagons, and fused hexagons, as illustrated in Figure 7. It becomes clear from our investigation that the cuboid with 20 hydrogen bonds is the most stable. The one represented as 12A is essentially a fusion of two cubes with D2dD2d symmetry (µ ) 0.0) and is clearly the most stable. A few other cuboid structures also exist for the 12-mer, out of which 12B and 12C with D2dS4 and S4S4 symmetries are slightly higher in energy by 0.27 and 0.55 kcal/mol, respectively. Both of the structures have nearly a zero dipole moment. A slightly distorted cuboid (12D) of D3 symmetry with µ ) 0.06 D, having two hydrogen bonds less than the cuboids 12A-C, is energetically much less stable. A fused hexameric structure (12E) of S6 symmetry is also less stable than the cuboids. The fused pentameric structure with two extensions (12G) also has only 18 bonds (two less than the cuboids) and is less stable than the cuboids and the fused hexamers, as depicted in Figure 7.
For (H2O)13, the most stable structure is an extension of the cuboid with an SE of -128.33 kcal/mol. It has 21 hydrogen bonds and is depicted in Figure 8 as 13A. The supermolecularbased as well as the pattern-based approach has been used to explore the possible structures of 13-mers. The other conformers that are energetically less stable, 13B-E, have SE ) -125.26, -125.07, -123.62, and -123.62 kcal/mol, respectively.
The various structures of (H2O)14 can be considered to arise from extensions of cuboids, pentagonoids, and their combinations. The structure 14A, which is a fusion of a cube and a fused pentamer, seems to be the most stable (SE ) -144.78 kcal/mol). The extended cuboid structure 14B is slightly higher in energy (SE ) -144.65 kcal/mol) than 14A but lower in energy than the fused pentamer-cuboid structure 14C (SE ) -131.20 kcal/mol). The structure 14D, with two cuboids sharing an edge, is still higher in energy (SE ) -130.09 kcal/mol). All of these structures are shown in Figure 9.
Figure 3. Schematic representation of some of the different possible low-energy structures of (H2O)8 along with the SE and nH values as obtained from HF/6-31G(d,p) calculations. The SE values in parentheses correspond to the results from DFT calculations using B3LYP parametrization.
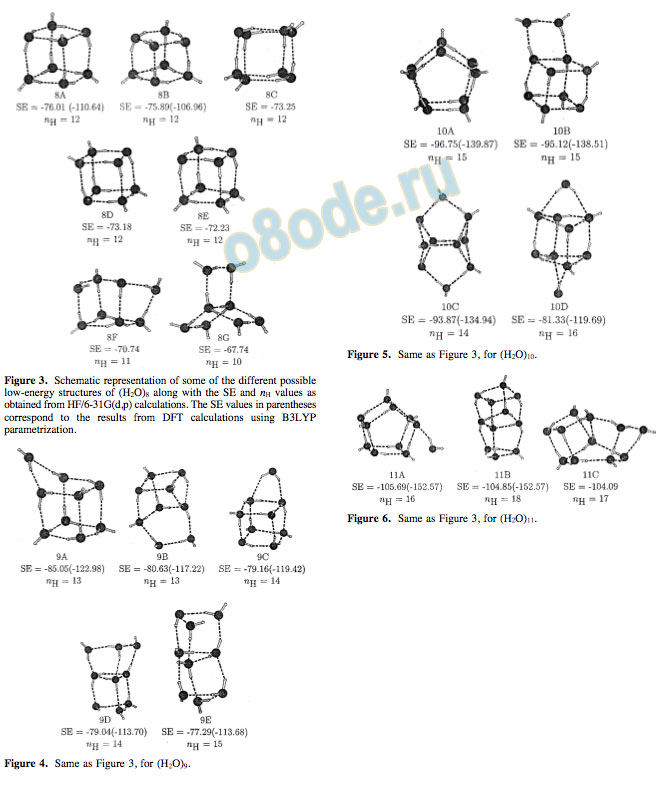
Figure 4. Same as Figure 3, for (H2O)9.
Figure 5. Same as Figure 3, for (H2O)10.
Figure 6. Same as Figure 3, for (H2O)11.
10530 J. Phys. Chem. A, Vol. 105, No. 46, 2001 Maheshwary et al.
On the basis of the structures of (H2O)5 and (H2O)10, we expected (H2O)15 to be a fused pentamer and found it to be so, with 26 hydrogen bonds, µ ) 4.46 D, and SE ) -154.82 kcal/ mol. The structure that comes closest in energy is a cuboid with the same number of hydrogen bonds and SE ) -152.40 kcal/ mol, as illustrated in Figure 10.Because (H2O)8 is a cube and (H2O)12 a fused cube, it is not surprising that the most stable geometry of (H2O)16 is a linear fused cube (16A). It is highly symmetrical (µ ) 0.0) with 28 hydrogen bonds and SE ) -169.33 kcal/mol. The branched cuboid (16E) has the same number of hydrogen bonds as 16A but is clearly higher in energy by 7.3 kcal/mol, as illustrated in Figure 11. Interestingly, a fused pentameric structure (16B), with the 16th water molecule hydrogen bonded to one of the corners, is intermediate in energy between 16A and 16C. Table 3 gives the details of the energetics at both the HF and DFT levels using the 6-31G(d,p) and 6-311++G(2d,2p) basis sets.
It can be seen from Figure 12 that the most stable structure (17A) for the 17-mer has one H2O hydrogen bonded to one of the corners of the linear cuboid that is the stable structure for the 16-mer. It has 29 hydrogen bonds and an SE of -176.51 kcal/mol. An alternative structure (17B) based on the fusion of

Figure 7. Same as Figure 3, for (H2O)12.
Figure 8. Same as Figure 3, for (H2O)13.
Figure 9. Same as Figure 3, for (H2O)14.
Figure 10. Same as Figure 3, for (H2O)15.
tetrameric and pentameric rings has 26 hydrogen bonds and is much higher in energy (SE ) -172.82 kcal/mol). Other structures (17C-E) with nearly comparable energies (SE ) -170.45, -170.44, and -169.57 kcal/mol, respectively) were also observed.
The most stable structure of the 18-mer (18A) is also an extension to the linear cuboid structure, as shown in Figure 13. There are two water molecules, each two-coordinated and hydrogen bonded to the two adjacent corners of the linear cuboid. It has 31 hydrogen bonds and an SE of -188.64 kcal/ mol. The alternative structure 18C is based on the cuboid. Despite the fact that it has 33 hydrogen bonds, it has a lower SE (-184.76 kcal/mol) than 18A. A linear cuboid structure (18B) with two water molecules hydrogen bonded to two nonadjacent oxygen atoms on the face of a linear cuboid structure is slightly more stable than 18C, emphasizing the stability of the linear cuboid structure. Yet, another alternative in the form of a fused pentamer structure (18D) turns out to be higher in energy than the cuboids.
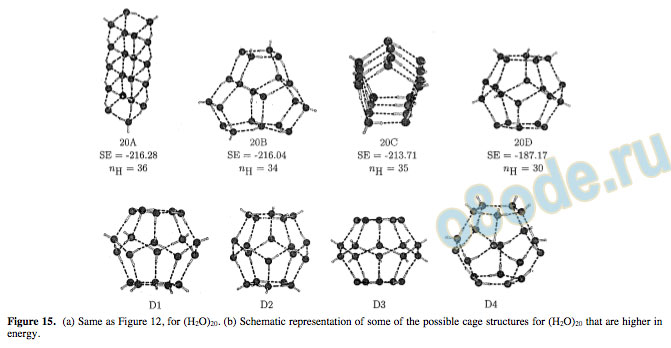
In the case of the 19-mer, the most stable structure is likely to be linked to the stability of the 20-mer (one corner missing from the cuboid or a pentagonoid). It turns out that the linear cuboid with a corner missing (19B) is slightly less stable (SE ) -199.41 kcal/mol) than the pentagonoid (19A) with a corner missing (SE ) -199.70 kcal/mol), as shown in Figure 14. The former has 35 hydrogen bonds, while the latter has 33. Other fused pentagonoids (19C and 19D) are much higher in energy. From the most stable geometries for the different n-mers of water discussed above, it becomes clear that when n is a multiple of 4, the structure based on the stacking of tetramer rings is the most stable, resulting in the cuboid for (H2O)8 and linear cuboid structures for (H2O)12 and (H2O)16. Therefore, we expect (H2O)20 also to be a linear cuboid in its lowest-energy form. However, we can also anticipate from the cyclic structure of (H2O)5 and the stacked pentagon structure for (H2O)10 and (H2O)15 that (H2O)20 would be made up of fused pentagons. In addition, from the work of Pauling on clathrates,85 one would expect a dodecahedral cage structure, which also results from the fusion of pentameric rings. Therefore, we have examined different classes of structures for the 20-mer, as illustrated in Figure 15a. It has 36 hydrogen bonds and an SE of -216.28 kcal/mol. The linearly stacked pentamer structure (20C) has only one hydrogen bond less and is slightly higher in energy by 2.57 kcal/mol. A “branched” fused pentameric structure (20B) is found to be slightly lower in energy by 2.33 kcal/mol than 20C but 0.24 kcal/mol higher than 20A. One could expect four different cage structures, D1-4, for (H2O)20, as shown in Figure 15b. They differ in the arrangement of the hydrogen atoms that are not involved in hydrogen bonding. Preliminary calculations using the 4-31G basis set showed D1 to be the most stable cage structure. Calculations at the HF/6-31G(d,p) level reveal its SE to be -187.17 kcal/mol, and therefore far less stable than 20A.
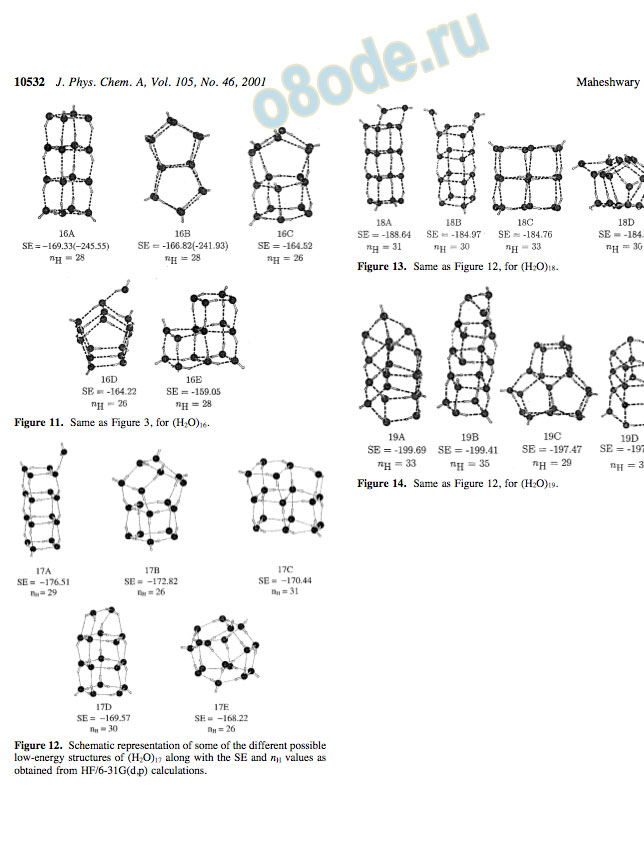
Figure 11. Same as Figure 3, for (H2O)16.
Figure 12. Schematic representation of some of the different possible low-energy structures of (H2O)17 along with the SE and nH values as obtained from HF/6-31G(d,p) calculations.
Figure 13. Same as Figure 12, for (H2O)18.
Figure 14. Same as Figure 12, for (H2O)19.
Because DFT calculations are being used extensively for the study of van der Waals and hydrogen-bonded clusters16,20,55 and B3LYP parametrization is often used, we have carried out DFT calculations with B3LYP parametrization using the 6-311++G(2d,2p) basis set for (H2O)n, n ) 2-8, and the 6-31G(d,p) basis set for (H2O)n, n ) 2-16. For n ) 2-6, our results are in agreement with the earlier reported DFT results.16,20 For n ) 6-16, our DFT calculations lead to the same set of stable geometries as HF. It is worth pointing out that, for n ) 11, DFT calculations show that the cuboid structure (with one corner missing) is essentially isoenergetic with the extended fused pentameric structure. We must also add that there are noticeable quantitative differences in the geometrical parameters for the different n-mers, as illustrated in Figure 16.
With an increase in the size of water clusters, the number of structural parameters also increases. Therefore, we have plotted the mean values r jO-Hb (Figure 16a), r jO‚‚‚O (Figure 16b), r jO‚‚‚H
(Figure 16c), and OHO (Figure 16d) along with their variations in the form of vertical bars for different values of n in Figure 16. For the n ) 2-5 clusters, there are only singledonor (sd) hydrogen bonds, whereas for n g 6, there are sd as well as double-donor (dd) hydrogen bonds. Figure 16a indicates that the values of r jO-Hb for dd hydrogen bonds are slightly shorter than those for sd bonds. For both categories (compare dd and sd), the HF values are consistently lower than the DFT values. The values of r jO‚‚‚O and r jO‚‚‚H predicted by HF calculations, however, are consistently larger than those from DFT calculations despite their overlapping variations, as shown in parts b and c of Figure 16. Figure 16d deals with the relation between the OHO value and the cluster size for n ) 2-16. It is nearly identical for both HF and DFT calculations, emphasizing the fact that the “shapes” of the most stable clusters predicted by the HF and DFT calculations are nearly the same. However, it must be added that DFT calculations tend to predict slightly stronger and shorter hydrogen bonds than those of HF.
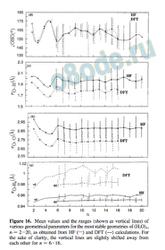
Figure 16. Mean values and the ranges (shown as vertical lines) of various geometrical parameters for the most stable geometries of (H2O)n, n ) 2-20, as obtained from HF (s) and DFT (---) calculations. For the sake of clarity, the vertical lines are slightly shifted away from each other for n ) 6-16.
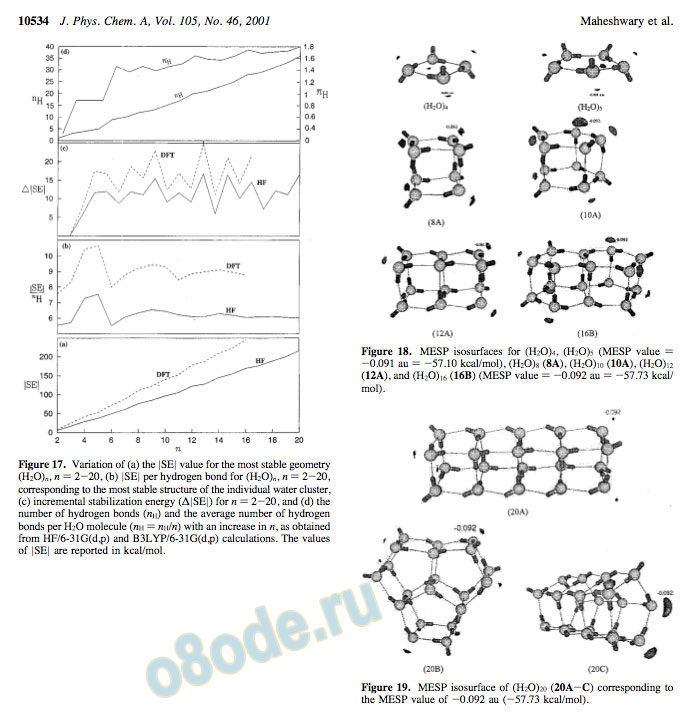
Structure and Stability of Water Clusters J. Phys. Chem. A, Vol. 105, No. 46, 2001 10533 as that for n ) 2. For n > 6, there is a slight increase in the mean hydrogen-bond strength until we reach the cuboid structure for n ) 8. With the further increase in the value of n, the change in the mean value is marginal, because most stable geometries are made up of cyclic tetramers and pentamers. It becomes clear from the incremental values of |SE| (i.e., the increase in |SE| values with the increase in n by 1) plotted as a function of n in Figure 17c that there is an alternation in stability as n increases. The even n-mers have a slightly greater stability than the odd n-mers. Water clusters with n ) 8, 12, 16, and 20 become particularly more stable. The average number of hydrogen bonds (njH) per water molecule increases with an increase in n initially but then levels off around 1.8 as n approaches 20. It is worth reiterating that the mean |SE| value also becomes approximately constant ( 6 kcal/mol at the HF level) as n approaches 20.
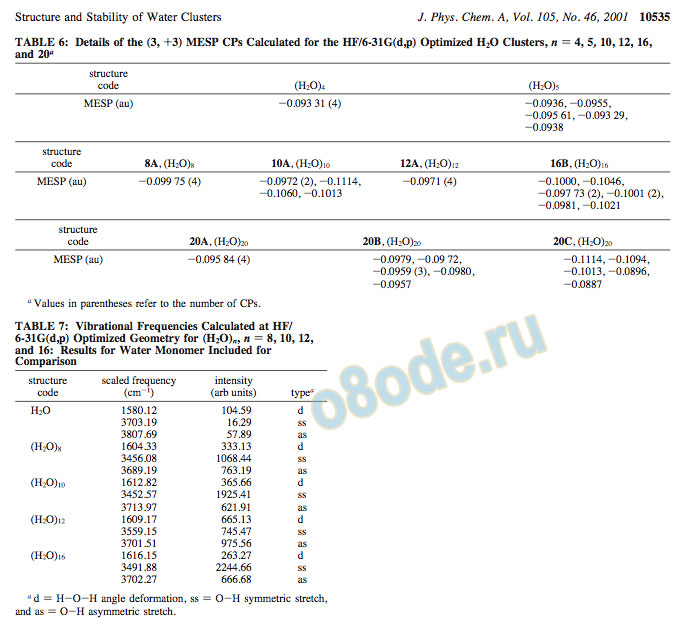
The MESP topography mapping of some of the (H2O)n clusters has been carried out at the HF/6-31G(d,p) level with a view to explore the reactivity features. The MESP isosurface (-57.73 kcal/mol) is displayed in Figures 18 and 19 for (H2O)n, n ) 4, 5, 8, 10, 12, 16, and 20 clusters. Details of the MESP CPs calculated for each system are given in Table 6. It can be seen that the MESP isosurfaces generated at a particular value, for the clusters containing pentameric rings (10A, 16B, and 20C), are larger than those of the clusters containing tetrameric rings (8A, 12A, and 20A). Therefore, it can be expected that the pentameric rings would be more reactive toward either a positively charged species (an electrophile) or a metal ion as compared to the tetrameric rings.
An attempt has been made to estimate the effect of BSSE and ZPE corrections on the |SE| at the HF level using the 6-311++G(2d,2p) basis set. It is clear from the results reported in Table 5 that the BSSE correction is about 10% of the |SE| for a given cluster, while the ZPE correction is about 40%.
However, they do not affect the conclusions regarding the shapes of clusters in most cases.
Frequency calculations have been carried out at the HF level employing the basis set 6-31G(d,p) for some of the important clusters comparing (H2O)8 (8A), (H2O)10 (10A), (H2O)12 (12A), and (H2O)16 (16B) and also using the 6-311++G(2d,2p) basis set for (H2O)n, n ) 2-10. These calculations reveal that all of the eigenvalues of the Hessian matrix are positive, and hence, the corresponding frequencies are real. This means that these structures are indeed (at least local) minima on the corresponding Figure 17. Variation of (a) the |SE| value for the most stable geometry (H2O)n, n ) 2-20, (b) |SE| per hydrogen bond for (H2O)n, n ) 2-20, corresponding to the most stable structure of the individual water cluster, (c) incremental stabilization energy ( |SE|) for n ) 2-20, and (d) the number of hydrogen bonds (nH) and the average number of hydrogen bonds per H2O molecule (nH ) nH/n) with an increase in n, as obtained from HF/6-31G(d,p) and B3LYP/6-31G(d,p) calculations. The values of |SE| are reported in kcal/mol.
Figure 18. MESP isosurfaces for (H2O)4, (H2O)5 (MESP value ) -0.091 au ) -57.10 kcal/mol), (H2O)8 (8A), (H2O)10 (10A), (H2O)12 (12A), and (H2O)16 (16B) (MESP value ) -0.092 au ) -57.73 kcal/ mol).
Figure 19. MESP isosurface of (H2O)20 (20A-C) corresponding to the MESP value of -0.092 au (-57.73 kcal/mol).
PESs. The scaling of the frequencies has been done with a scaling factor86 of 0.8929, as recommended by the GAUSSIAN94 package. Table 7 lists the scaled frequencies (cm-1) with maximum intensities for some of these clusters along with the frequencies of a single water molecule. The H-O-H angle deformation frequency is observed to generally increase on cluster formation. The O-H stretching (asymmetric as well as symmetric) frequencies, on the other hand, generally decrease with increasing cluster size. Also, it is noticed from Table 7 that the intensities of all of these vibrations are enhanced on cluster formation.
4. Summary and Conclusion
We have reported the results of a systematic investigation of water clusters (n ) 2-20) at ab initio levels using HF calculations with the 6-31G(d,p) and 6-311++G(2d,2p) basis sets. It has been observed that the tetrameric ring-based structures are more stable for n ) 8, 12, and 16, in agreement with the results of Lee et al.69b For n ) 10 and 15, pentameric ring-based structures are the most favored. For n ) 20, the linear cuboid is slightly more stable (by 0.24 kcal/mol at the HF/631G(d,p) level) than the fused pentameric structure. For intermediate values of n (9, 11, 13, 14, and 17-19), one finds the extended cuboid or extended fused pentameric structures to be the most stable. DFT calculations using B3LYP parametrization at the 6-31G(d,p) level reinforce our findings for (H2O)n, n ) 6-16.
Calculations at the HF level with different basis sets ranging from 6-31G(d,p) to 6-311++G (2d,2p) show a slight change in the SE values with the change of the basis set. For a given cluster optimized at the HF/6-311++G(2d,2p) level, the stabilization energy has been found to be lowered by 30% of its value at the HF/6-31G(d,p) level. Similar trends have been observed for the calculations at MP2 as well as the DFT/B3LYP levels with the 6-311++G(2d,2p) basis set. However, the overall trends in the energetics (with a few exceptions for which some of the structures converge to similar structures or the energy difference is very small) remain unaltered with the change in the basis set or the level of theory. With the sufficiently large basis set 6-311++G(2d,2p) used in this study, the BSSE correction is found to be 10% of the stabilization energy, while the ZPE correction at the same level is 40%.
We do realize that there are a large number of alternative geometries that are possible for the larger clusters, with the number increasing rapidly with an increase in cluster size. While consideration of all such geometries is beyond the scope of the present investigation, we did examine many alternative geometries and found them to be energetically much higher in energy than the structures reported in this study. Furthermore, frequency calculations for some of the most stable geometries confirm that they indeed correspond to (at least local) minima. Therefore, we believe that our results are definitive.
It has been observed that both of the modes of the O-H stretching frequencies tend to decrease on cluster formation, while the frequency of the H-O-H angle deformation tends to increase. All of these changes are accompanied by an enhancement in spectral density values with an increase in cluster size.
It can be seen from our study that the most stable geometries of water clusters contain tetrameric or pentameric rings. MESP values of the pentameric ring-based structures indicate the presence of a more negative-valued environment around them as compared to those of the tetrameric rings. It may be concluded from the MESP maps that (H2O)n clusters containing pentameric rings would react more favorably with electrophilic species. The same fact has been highlighted by the study of MESP CPs. The MESP topography study shows that the minima for the clusters with pentameric rings, (compare 10A, 16B, and
TABLE 6: Details of the (3, +3) MESP CPs Calculated for the HF/6-31G(d,p) Optimized H2O Clusters, n ) 4, 5, 10, 12, 16, and 20a
d ) H-O-H angle deformation, ss ) O-H symmetric stretch, and as ) O-H asymmetric stretch.
20C) are deeper by -69.03 kcal/mol than those of tetrameric rings. Also, the electrostatics-based studies on molecular hydration87 support this prediction. The MESP maps for water clusters with n ) 8, 10, 12, 15, 16, and 20 suggest that the smaller clusters with n ) 4, 5, and 8 can be used as the basic building blocks for generating larger clusters. Some of the cage structures reported in this study may be of importance in the entrapment of molecules.
Acknowledgment. This study evolved from a classroom project at IIT Kanpur and we thank the students enrolled in the course (Chm621 Chemical Binding) for some of the early investigations. We are grateful to E. Arunan (IISc, Bangalore), S. Manogaran (IIT Kanpur), S. P. Gejji, and R. K. Pathak (University of Pune) for valuable discussions during the course of this study. This study was supported in part by a Senior Research Fellowship to S.M. from the Council of Scientific and Industrial Research, New Delhi, India. Support from the Centre for Development of Advanced Computing (C-DAC), Pune, India, is gratefully acknowledged. We are also thankful to J. Coe (Ohio State University, Columbus, OH) and B. Hartke (Stuttgart, Germany) for useful data and discussions on water clusters.
References and Notes
(1) Liu, K.; Cruzan, J. D.; Saykally, R. J. Science 1996, 271, 929.
(2) Wales, D. J. In Encyclopaedia of Computational Chemistry; Schleyer, P. v. R., Allinger, N. L., Clark, T., Gasteiger, J., Kollman, P. A., Schaefer, H. F., III, Schreiner, P. R., Eds.; Wiley: New York, 1998; Vol. 5, p 3183.
(3) Mu¨ ller-Dethlefs, K.; Hobza, P. Chem. ReV. 2000, 100, 143.
(4) Ugalde, J. M.; Alkorta, I.; Elguero, J. Angew. Chem., Int. Ed. 2000, 39, 717.
(5) Dyke, T. R.; Muenter, J. S. J. Chem. Phys. 1974, 60, 2929.
(6) Dyke, T. R.; Mack, K. M.; Muenter, J. S. J. Chem. Phys. 1977, 66, 498 and references therein.
(7) Odutola, J. A.; Dyke, T. R. J. Chem. Phys. 1980, 72, 5062.
(8) Fraser, G. T. Int. ReV. Phys. Chem. 1991, 10, 189.
(9) Feller, D. J. Chem. Phys. 1992, 96, 6104.
(10) Pugliano, N.; Cruzan, J. D.; Loeser, J. G.; Saykally, R. J. J. Chem. Phys. 1993, 98, 6600.
(11) Pribble, R. N.; Zwier, T. S. Science 1994, 265, 75.
(12) Honegger, E.; Leutwyler, S. J. Chem. Phys. 1988, 88, 2582.
(13) Smith, B. J.; Swanton, D. J.; Pople, J. A.; Schaefer, H. F., III; Random, L. J. Chem. Phys. 1990, 92, 1240.
(14) Millot, C.; Stone, A. J. Mol. Phys. 1992, 77, 439.
(15) Xantheas, S. S.; Dunning, T. H., Jr. J. Chem. Phys. 1993, 99, 8774.
(16) Laasonen, K.; Parinello, M.; Car, R.; Lee, C.; Vanderbilt, D. Chem. Phys. Lett. 1993, 207, 208.
(17) Chakravorty, S. J.; Davidson, E. R. J. Phys. Chem. 1993, 97, 6373.
(18) Scheiner, S. Annu. ReV. Phys. Chem. 1994, 45, 23.
(19) Xantheas, S. S. J. Chem. Phys. 1994, 100, 7523.
(20) Feyereisen, M. W.; Feller, D.; Dixon, D. A. J. Phys. Chem. 1996, 100, 2993.
(21) Estrin, D. A.; Paglieri, L.; Corongiu, G.; Clementi, E. J. Phys. Chem. 1996, 100, 8701.
(22) Xantheas, S. S. J. Chem. Phys. 1996, 104, 8821.
(23) Gregory, J. K.; Clary, D. C. J. Phys. Chem. 1996, 100, 18014.
(24) Schu¨ tz, M.; Rauhut, G.; Werner, H.-J. J. Phys. Chem. A 1998, 102, 5997.
(25) Millot, C.; Soetens, J. C.; Costa, M. T. C. M.; Hodges, M. P.; Stone, A. J. J. Phys. Chem. A 1998, 102, 754.
(26) Bentwood, R. M.; Barnes, A. J.; Orville-Thomas, W. A. J. Mol. Spectrosc. 1980, 84, 391.
(27) Del Bene, J. E.; Pople, J. A. J. Chem. Phys. 1970, 52, 4858.
(28) Dyke, T. R.; Muenter, J. S. J. Chem. Phys. 1972, 57, 5011.
(29) Pugliano, N.; Saykally, R. J. Science 1992, 257, 1937.
(30) Viant, M. R.; Cruzan, J. D.; Lucas, D. D.; Brown, M. G.; Liu, K.; Saykally, R. J. J. Phys. Chem. A 1997, 101, 9032.
(31) Mo´ , O.; Ya´ nez, M.; Elguero, J. J. Chem. Phys. 1992, 97, 6628.
(32) Wales, D. J. J. Am. Chem. Soc. 1993, 115, 11180.
(33) Schu¨ tz, M.; Bu¨ rgi, T.; Leutwyler, S.; Bu¨ rgi, H. B. J. Chem. Phys. 1993, 99, 5228; 1994, 100, 1780(E).
(34) Xantheas, S. S.; Dunning, T. H., Jr. J. Chem. Phys. 1993, 98, 8037.
(35) Fowler, J. E.; Schaefer, H. F., III. J. Am. Chem. Soc. 1995, 117, 446.
(36) Klopper, W.; Schu¨ tz, M.; Lu¨ thi, H. P.; Leutwyler, S. J. Chem. Phys. 1995, 103, 1085.
(37) Hodges, M. P.; Stone, A. J.; Xantheas, S. S. J. Phys. Chem. A 1997, 101, 9163.
(38) (a) Masella, M.; Flament, J.-P. J. Chem. Phys. 1997, 107, 9105. (b) Masella, M.; Flament, J.-P. J. Chem. Phys. 1999, 110, 7245.
(39) Nielsen, I. M. B.; Seidi, E. T.; Janssen, C. L. J. Chem. Phys. 1999, 110, 9435.
(40) Kim, K. S.; Dupuis, M.; Lie, G. C.; Clementi, E. Chem. Phys. Lett. 1986, 131, 451.
(41) Schu¨ tz, M.; Klopper, W.; Lu¨ thi, H. P.; Leutwyler, S. J. Chem. Phys. 1995, 103, 6114.
(42) Cruzan, J. D.; Braly, L. B.; Liu, K.; Brown, M. G.; Loeser, J. G.; Saykally, R. J. Science 1996, 271, 59.
(43) Cruzan, J. D.; Braly, L. B.; Liu, K.; Brown, M. G.; Loeser, J. G.; Saykally, R. J. J. Phys. Chem. A 1997, 101, 9022.
(44) Liu, K.; Brown, M. G.; Cruzan, J. D.; Saykally, R. J. J. Phys. Chem. A 1997, 101, 9011.
(45) Cruzan, J. D.; Viant, M. R.; Brown, M. G.; Lucas, D. D.; Liu, K.; Saykally, R. J. Chem. Phys. Lett. 1998, 292, 667.
(46) Brown, M. G.; Keutsch, F. N.; Saykally, R. J. J. Chem. Phys. 1998, 109, 9645.
(47) Knochenmuss, R.; Leutwyler, S. J. Chem. Phys. 1992, 96, 5233.
(48) Burke, L. A.; Jensen, J. O.; Jensen, J. L.; Krishanan, P. N. Chem. Phys. Lett. 1993, 206, 293.
(49) Wales, D. J. Science 1996, 271, 925.
(50) Mhin, B. J.; Kim, H. S.; Yoon, C. W.; Kim, K. S. Chem. Phys. Lett. 1991, 176, 41.
(51) Krishnan, P. N.; Jensen, J. O.; Burke, L. A. Chem. Phys. Lett. 1994, 217, 311.
(52) Tsai, C. J.; Jordan, K. D. Chem. Phys. Lett. 1993, 213, 181.
(53) Kim, K. S.; Jordan, K. D.; Zwier, T. S. J. Am. Chem. Soc. 1994, 116, 11568.
(54) Mhin, B. J.; Kim, J.; Lee, S.; Lee, J. Y.; Kim, K. S. J. Chem. Phys. 1994, 100, 4484.
(55) Lee, C.; Chen, H.; Fitzgerald, G. J. Chem. Phys. 1994, 101, 4472.
(56) Kim, J.; Kim, K. S. J. Chem. Phys. 1998, 109, 5886.
(57) Kryachko, E. S. Int. J. Quantum Chem. 1998, 70, 831.
(58) (a) Kryachko, E. S. Int. J. Quantum Chem. 1999, 314, 353. (b) Tissandier, M. D.; Singer, S. J.; Coe, J. V. J. Phys. Chem. A 2000, 104, 752.
(59) Liu, K.; Brown, M. G.; Carter, C.; Saykally, R. J.; Gregory, J. K.; Clary, D. C. Nature 1996, 381, 501.
(60) Liu, K.; Brown, M. G.; Cruzan, J. D.; Saykally, R. J. J. Phys. Chem. A 1997, 101, 8995.
(61) Gregory, J. K.; Clary, D. C. J. Phys. Chem. A 1997, 101, 6813.
(62) Janzen, Ch.; Spangenberg, D.; Roth, W.; Kleinermanns, K. J. Chem. Phys. 1999, 110, 9898.
(63) Brudermann, J.; Melzer, M.; Buck, U.; Kazimirski, J. K.; Sadlej, J.; Bush, V. J. Chem. Phys. 1999, 110, 10649.
(64) Jensen, J. O.; Krishnan, P. N.; Burke, L. A. Chem. Phys. Lett. 1995, 241, 253.
(65) Kryachko, E. S. Chem. Phys. Lett. 1997, 272, 132.
(66) Kim, J.; Mujumdar, D.; Lee, H. M.; Kim, K. S. J. Chem. Phys. 1999, 110, 9128.
(67) Jensen, J. O.; Krishnan, P. N.; Burke, L. A. Chem. Phys. Lett. 1995, 246, 13.
(68) Kim, J.; Mhin, B. J.; Lee, S. J.; Kim, K. S. Chem. Phys. Lett. 1994, 219, 243.
(69) (a) Buck, U.; Ettischer, I.; Melzer, M.; Buch, V.; Sadlej, V. Phys. ReV. Lett. 1998, 80, 2578. (b) Lee, C.; Chen, H.; Fitzgerald, G. J. Chem. Phys. 1995, 102, 1266 and references therein.
(70) Gruenloh, C. J.; Carney, J. R.; Arrington, C. A.; Zwier, T. S.; Fredericks, S. Y.; Jordan, K. D. Science 1997, 276, 1678.
(71) Jensen, J. O.; Krishnan, P. N.; Burke, L. A. Chem. Phys. Lett. 1996, 260, 499.
(72) Tsai, C. J.; Jordan, K. D. J. Phys. Chem. 1993, 97, 5208.
(73) Jorgensen, W. L.; Chandrasekhar, J.; Madura, J. D.; Impey, R. W.; Klein, M. L. J. Chem. Phys. 1983, 79, 926.
(74) Sremaniak, L. S.; Perera, L.; Berkowitz, M. L. J. Chem. Phys. 1996, 105, 3715.
(75) Moore Plummer, P. L. J. Mol. Struct.: THEOCHEM 1997, 417, 35.
(76) Kirschner, K. N.; Shields, G. C. Int. J. Quantum Chem. 1994, 28, 349
(77) Khan, A. J. Phys. Chem. 1995, 99, 12450 and references therein.
(78) (a) Khan, A. Chem. Phys. Lett. 1996, 253, 299. (b) Khan, A. J. Chem. Phys. 1997, 106, 5537. (c) Khan, A. J. Phys. Chem. A 1999, 103, 1260 and references therein.
(79) Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Gill, P. M. W.; Johnson, B. G.; Robb, M. A.; Cheeseman, J. R.; Keith, T.; Petersson, G. A.; Montgomery, J. A.; Raghavachari, K.; Al-Laham, M. A.; Zakrzewski, V. G.; Ortiz, J. V.; Foresman, J. B.; Cioslowski, J.; Stefanov, B. B.; 10536 J. Phys. Chem. A, Vol. 105, No. 46, 2001 Maheshwary et al. Nanayakkara, A.; Challacombe, M.; Peng, C. Y.; Ayala, P. Y.; Chen, W.; Wong, M. W.; Andres, J. L.; Replogle, E. S.; Gomperts, R.; Martin, R. L.; Fox, D. J.; Binkley, J. S.; Defrees, D. J.; Baker, J.; Stewart, J. P.; HeadGordon, M.; Gonzalez, C.; Pople, J. A. Gaussian94, Revision C.2; Gaussian Inc.: Pittsburgh, PA, 1995.
(80) (a) Gadre, S. R. In Computational Chemistry: ReViews of Current Trends; Lesczynski, J., Ed.; World Scientific: River Edge, NJ, 2000; Vol. 4. (b) Gadre, S. R.; Shirsat, R. N. Electrostatics of Atoms and Molecules; Universities Press: Hyderabad, India, 2000 and references therein.
(81) Bapat, S. V.; Shirsat, R. N.; Gadre, S. R. UNIPROP; Molecular Property Calculation Package Developed by the Theoretical Chemistry Group, Department of Chemistry, University of Pune, Pune, India. Chem. Phys. Lett. 1992, 200, 373.
(82) Limaye, A. C.; Gadre, S. R. UNIVIS-2000; Molecular Properties Visualization Package Developed by the Theoretical Chemistry Group, Department of Chemistry, University of Pune, Pune, India. Curr. Sci. 2001, 80, 1296.
(83) (a) Hoy, R.; Bunker, P. R. J. Mol. Spectrosc. 1975, 59, 159. (b) Turi, L.; Dannenberg, J. J. J. Phys. Chem. 1995, 99, 639. (c) Wong, N.-B.; Cheung, Y.-S.; Wu, D. Y.; Ren, Y.; Wang, X.; Tian, A. M.; Li, W.-K. J. Mol. Struct. 2000, 507, 153.
(84) Jeffrey, G. A.; Saenger, W. Hydrogen Bonding in Biological Structures; Springer-Verlag: New York, 1991. Jeffrey, G. A. An Introduction to Hydrogen Bonding; Oxford University Press: Oxford, 1997.
(85) Pauling, L. The Nature of the Chemical Bond, 3rd ed; Cornell University Press: Ithaca, NY, 1960; p 469.
(86) Foresman, J. B.; Frisch, A. Exploring Chemistry with Electronic Structure Methods: A Guide to Using Gaussian; Gaussian Inc.: Pittsburgh, PA, 1993.
(87) Gadre, S. R.; Kulkarni, A. D. Unpublished results.
Structure and Stability of Water Clusters J. Phys. Chem. A, Vol. 105, No. 46, 2001 10537